Hans Walser, [20220116]

Dreiecke im n-Eck

Anregung: Swetlana Nordheimer, Bonn

1 Problemstellung

Zu n Punkten zeichnen wir alle Verbindungsgeraden und fragen nach der (maximal möglichen) Anzahl der Dreiecke, welche durch diese Geraden gebildet werden.

2 Beispiel

Zu n = 4 Punkten gibt es sechs Geraden (Abb. 1a). Wir bezeichnen diese gemäß Abbildung 1b.

Abb. 1: Vier Punkte und sechs Geraden

Die Dreiecke zeichnen wir in der Reihenfolge der Tabelle 1. Die hellblau unterlegten Fälle sind ausgeschlossen, da die betreffenden drei Geraden durch denselben Punkt verlaufen (einer der vier gegebenen Punkte).

abc	abd	abe	abf
acd	ace	acf
ade	adf
aef
bcd	bce	bcf
bde	bdf
bef
cde	cdf
cef
def

Tab. 1: Dreiecke

Die Abbildung 2 zeigt die 16 Dreiecke. Die ausgeschlossenen Fälle sind durch einen hellblauen Punkt markiert.

Abb. 2: 16 Dreiecke

3 Allgemein

Zu n Startpunkten gibt es

(1)

Geraden. Aus diesen Geraden können wir

(2)

Tripel auswählen. Es bilden aber nicht alle Tripel ein Dreieck. Durch jeden der n Startpunkte verlaufen n – 1 Geraden. Somit haben wir in jedem Startpunkt

(3)

Tripel, welche kein Dreieck bilden. Für die gesuchte maximal mögliche Anzahl f(n) Dreiecke ergibt sich daher:

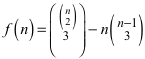(4)

Die Tabelle 2 gibt die ersten Werte.

n	f(n)	n	f(n)
1	0	11	24915
2	0	12	43780
3	1	13	73216
4	16	14	117481
5	100	15	182000
6	395	16	273560
7	1190	17	400520
8	2996	18	573036
9	6636	19	803301
10	13350	20	1105800

Tab. 2: Erste Werte

4 Technisches

Der Ausdruck (4) ist eine Polynomfunktion in n vom Grad 6:

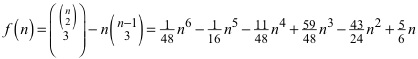(5)

Website

Hans Walser: Dreiecke im Siebeneck

http://www.walser-h-m.ch/hans/Miniaturen/D/Dreiecke_im_Siebeneck/Dreiecke_im_Siebeneck.html