Hans Walser, [20200228]
Dreiecke und Quadrate
Idee und Anregung: Thomas Jahre, Serie 53 – 632. Aufgabe
1 Problemstellung
ãSind die Kanten der gleichseitigen Dreiecke und der Quadrate, die du ausgeschnitten hast, alle gleich gro§?Ò, fragte Bernd seine Schwester.
ãJa, die haben alle die gleiche Kantenlnge. Ich lege daraus Figuren und ermittle die Anzahl der Ecken. Ich nehme so viele von den Dreiecken oder Quadraten wie ich mchte. Schn Kante an Kante legen.Ò
Quadrat + Quadrat ergibt ein Rechteck, das hat 4 Ecken. Dreieck + Dreieck ergibt ein Rhombus, das hat auch 4 Ecken. Ein Quadrat + ein Dreieck ergibt ein 5-Eck, das, wie der Name sagt, 5 Ecken hat. Was man kombiniert, ist beliebig, die Figur darf aber keine Lcher haben und soll konvex sein.
Bernd meint, aus den vielen Dreiecke und Quadraten lie§e sich bestimmt jedes konvexe n-Eck legen (n > 2), wenn man nur lange genug probiert. Hat er Recht?
2 Bearbeitung
Die Abbildung 1 zeigt exemplarisch Beispiele fr die Eckenzahlen von 3 bis 12.
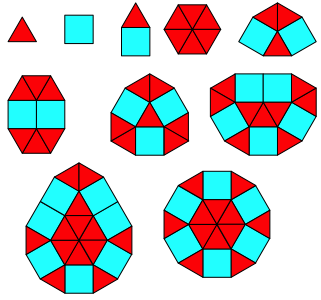
Abb. 1: Beispiele
Es gibt keine Beispiele fr Eckenzahlen n > 12. Dies zeigen wir mit Au§enwinkeln.
3 Au§enwinkel
Fr unsere Figuren kommen nur die Au§enwinkel 120¡, 90¡, 60¡ und 30¡ in Frage (Abb. 2).
![]()
Abb. 2: Au§enwinkel
Die Au§enwinkelsumme eines Vieleckes ist 360¡.
Da die Au§enwinkel mindestens 30¡ messen, kann es hchstens 12 Ecken geben.
4 Ringe ansetzen
Wir vergr§ern die Figuren der Abbildung 1 unter Beibehaltung der Eckenkonfiguration. Die Vergr§erung geschieht durch Ansetzen von Ringen nach einem einheitlichen Schema (Abb. 3).
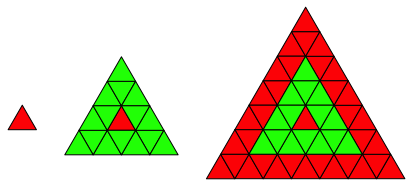
Abb. 3.1: Drei Ecken
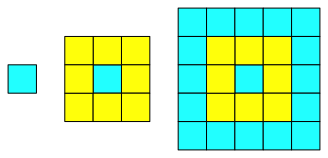
Abb. 3.2: Vier Ecken
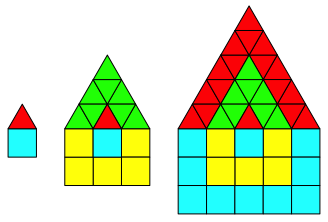
Abb. 3.3: Fnf Ecken
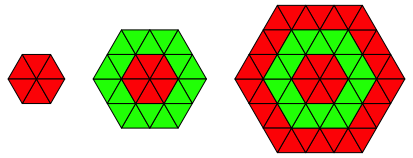
Abb. 3.4: Sechs Ecken
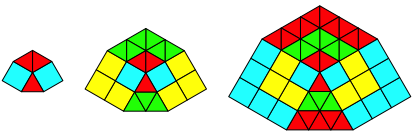
Abb. 3.5: Sieben Ecken
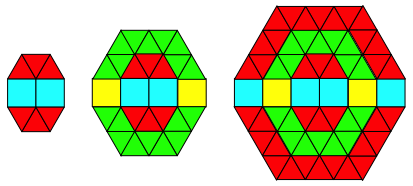
Abb. 3.6: Acht Ecken
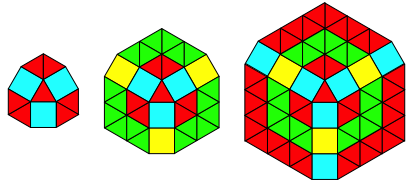
Abb. 3.7: Neun Ecken
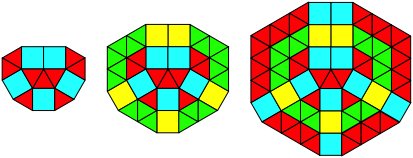
Abb. 3.8: Zehn Ecken
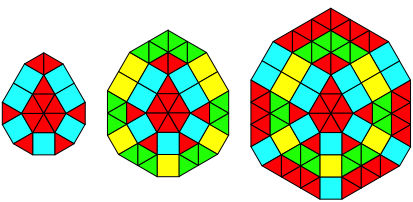
Abb. 3.9: Elf Ecken
Bei zwlf Ecken gibt es verschiedene Varianten. Die Abbildungen 3.10 und 3.11 zeigen zwei Beispiele.
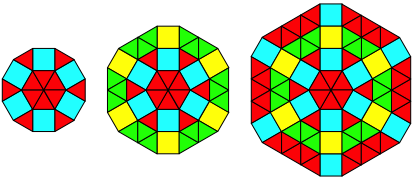
Abb. 3.10: Zwlf Ecken
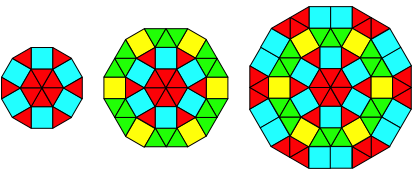
Abb. 3.11: Zwlf Ecken, Variante
Die Abbildung 3.12 zeigt eine ausfhrlichere Variante.
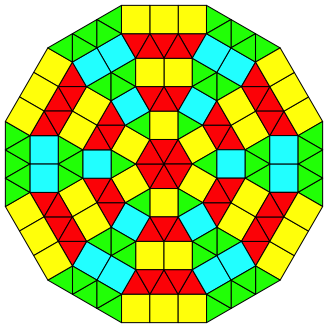
Abb. 3.12: Zwlf Ecken
Website
https://www.schulmodell.eu/aufgabe-der-woche.html