Hans Walser, [20220701]

Dreiecksaufgabe

1 Aufgabenstellung

Von einem Dreieck ABC kennen wir die Ecke A, den Umkreismittelpunkt U und den Höhenschnittpunkt H.

Gesucht ist das Dreieck ABC.

2 Bearbeitung

2.1 Lösung mit Euler-Gerade

Abb. 1: Lösung mit Euler-Gerade

Nr.	Name	Beschreibung	Bemerkungen
1	Punkt A		Gegebene Dreiecksecke A
2	Punkt U		Gegebener Umkreismittelpunkt
3	Punkt H		Gegebener Höhenschnittpunkt
4	Gerade e	Line U, H	Euler-Gerade
5	Punkt S	H zentrisch gestreckt um Faktor 1 / 3 von U aus	Schwerpunkt
6	Punkt Ma	S zentrisch gestreckt um Faktor 3 / 2 von A aus	Mittelpunkt der Seite a
7	Kreis u	Kreis durch A mit Mittelpunkt U	Umkreis
8	Kreis u'	u gespiegelt an Ma
9	Punkt B	Schnittpfad von u, u'	Dreiecksecke B
10	Punkt C	Schnittpfad von u, u'	Dreiecksecke C
11	Dreieck d1	Polygon A, B, C	Dreieck ABC
11	Strecke c	Strecke A, B
11	Strecke a	Strecke B, C
11	Strecke b	Strecke C, A

Created with GeoGebra

Der Konstruktionsweg ergibt sich aus Eigenschaften der Euler-Gerade.

2.2 Zweiter Lösungsweg

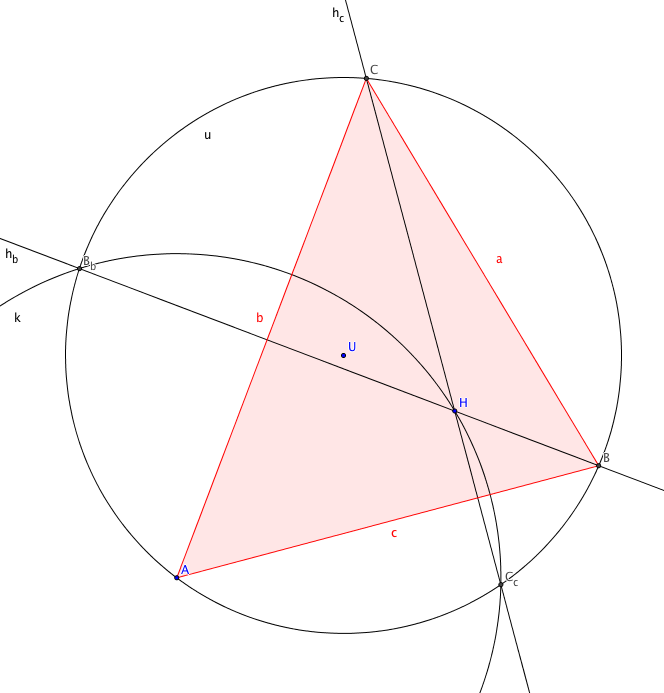
Nr.	Name	Beschreibung	Bemerkungen
1	Punkt A		Gegebene Dreiecksecke A
2	Punkt U		Gegebener Umkreismittelpunkt
3	Punkt H		Gegebener Höhenschnittpunkt
4	Kreis u	Kreis durch A mit Mittelpunkt U	Umkreis
5	Kreis k	Kreis durch H mit Mittelpunkt A	Schlüsselkreis
6	Punkt Bb	Schnittpfad von u, k
7	Punkt Cc	Schnittpfad von u, k
8	Gerade hb	Line Bb, H	Höhe hb (Trägergerade)
9	Gerade hc	Line Cc, H	Höhe hc (Trägergerade)
10	Punkt B	Schnittpfad von u, hb	Dreiecksecke B
11	Punkt C	Schnittpfad von u, hc	Dreiecksecke C
12	Dreieck d1	Polygon A, B, C	Dreieck ABC
12	Strecke c	Strecke A, B
12	Strecke a	Strecke B, C
12	Strecke b	Strecke C, A

Created with GeoGebra

Der Konstruktionsweg ergibt sich aus Winkelüberlegungen.