Hans Walser, [20190302]
Dreiecksaufwicklung
1 Worum geht es?
Spiel mit einem Gelenkmodell. Fhrt zu einer einfach berechenbaren Situation, die aber mit Zirkel und Lineal nicht lsbar ist.
2 Das Gelenkmodell
Wir denken uns ein Gelenkmodell mit drei gleich langen Stben und jeweils gleichen Gelenkwinkeln (Abb. 1). Wir arbeiten dabei mit den Au§enwinkeln.
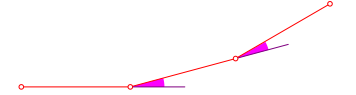
Abb. 1: Gelenkmodell
3 Aufwickeln zum Dreieck
Wir legen den ersten Stab horizontal hin und vergr§ern den Au§enwinkel, bei 0¡ beginnend, bis sich das Gelenkmodell zum gleichseitigen Dreieck schlie§t. Dies ist beim Au§enwinkel 120¡ der Fall (Abb. 2).

Abb. 2: Schlie§en zum gleichseitigen Dreieck
4 Bahnkurven der Gelenke
Der Startpunkt und das erste Gelenk bleiben fest. Das zweite Gelenk bewegt sich auf einem Kreis (blau in Abb. 3). Der Endpunkt bewegt sich auf einer Kurve, die aus einer berlagerung zweiter Kreisbewegungen besteht (grn in Abb. 3). Die Bahnkurven sind fr einen Parameterbereich (Au§enwinkel) von –180¡ bis 180¡ gezeichnet.
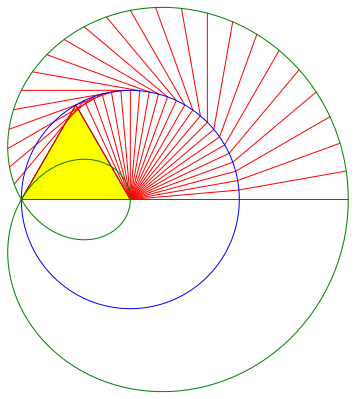
Abb. 3: Bahnkurven
5 Kollision an der Spitze
Wir sehen, dass der dritte Stab des Gelenkmodells bei der Bewegung zeitweise die Spitze des Dreiecks abschneidet.
In welcher Position touchiert der dritte Stab die Dreiecksspitze (Abb. 4a)? Wir suchen den zugehrigen Au§enwinkel t.
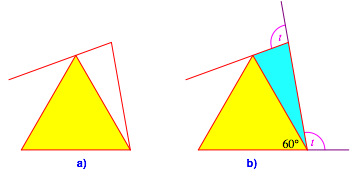
Abb. 4: Kollision an der Spitze
Das in der Abbildung 4b hellblau eingezeichnete Dreieck ist gleichschenklig. Sein Basiswinkel ist 180¡ – t, sein Spitzenwinkel 180¡ – 60¡ – t. Aus der Winkelsumme 180¡ erhalten wir:
![]() (1)
(1)
Eine ganz einfache Rechnung mit einem schnen Resultat. Nur: ein Winkel von 100¡ ist nicht mit Zirkel und Lineal konstruierbar.
Wenn wir einen Winkel von 100¡ mit Zirkel und Lineal konstruieren knnten, knnen wir zunchst einen Winkel von 60¡ subtrahieren (mit Zirkel und Lineal machbar) und htten einen Winkel von 40¡. Dies ist der Zentriwinkel des regelm§igen Neunecks, das wir somit mit Zirkel und Lineal konstruieren knnten. Das widerspricht aber einem Satz von Gau§ ber die Konstruierbarkeit regelm§iger Vielecke.
Wir knnen also die Situation der Abbildung 4a nicht mit Zirkel und Lineal konstruieren.
Bei einem rechnerischen Zugang zu diesem Problem treffen wir auf kubische Gleichungen.
6 Quadrat und regelm§iges Fnfeck
Die Abbildung 5 zeigt die entsprechende Figur fr das Quadrat.
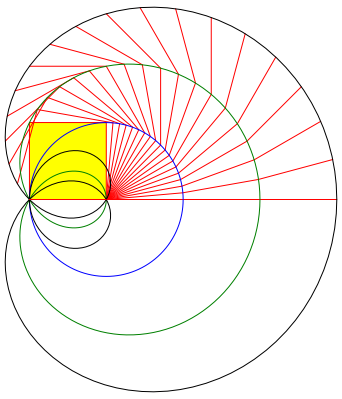
Abb. 5: Gelenkmodell mit vier Teilen
Die Kollision tritt bei einem Au§enwinkel von etwa 77.32658862¡ ein (Abb. 6).

Abb. 6: Kollision
Die Abbildung 7 zeigt die entsprechende Situation beim regelm§igen Fnfeck.
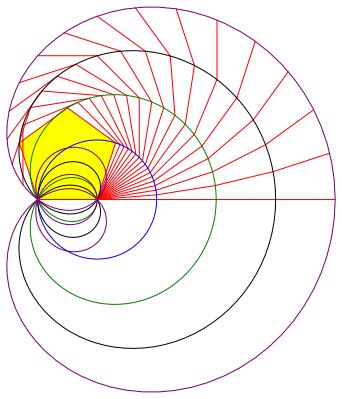
Abb. 7: Gelenkmodell mit fnf Teilen
Die Kollision tritt bei einem Au§enwinkel von etwa 63.165¡ ein (Abb. 8).

Abb. 8: Kollision