Hans Walser, [20230313]

Dreiecksspirale

Anregung: Thomas Jahre, Aufgabe 62 - 741

1 Worum geht es?

Aus rechtwinkligen Dreiecken und Quadraten aufgebaute eckige logarithmische Spiralen.

2 Konstruktionsvorgang

2.1 Dreieck und Quadrat

In ein beliebiges rechtwinkliges Dreieck passen wir das Quadrat ein, das auf der Hypotenuse aufsitzt (Abb. 1).

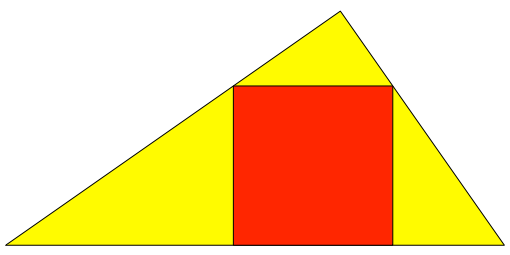
Abb. 1: Quadrat im rechtwinkligen Dreieck.

Die Konstruktion ist einfach: wir ziehen das Hypotenusenquadrat hinein (Perspektivabbildung, zentrische Streckung).

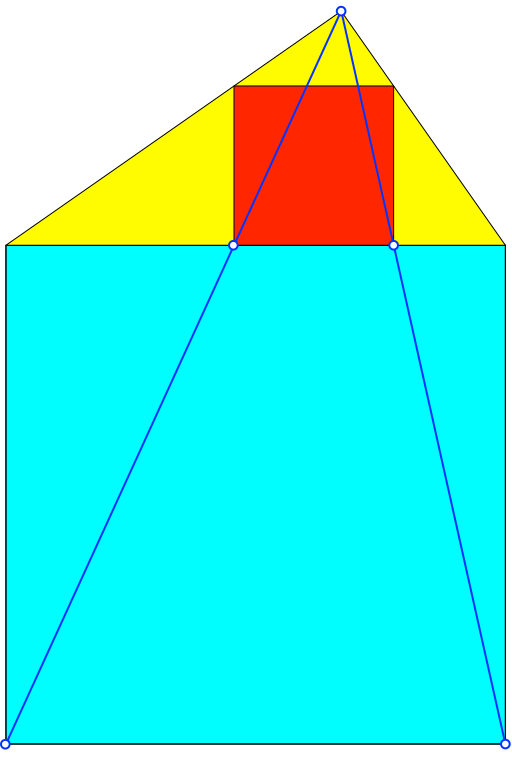
Abb. 2: Konstruktion mit Hypotenusenquadrat

2.2 Dreieck ansetzen

Wir ergänzen das rechtwinklige Dreieck durch ein kleineres ähnliches Dreieck zu einem größeren ähnlichen Dreieck (Abb. 3). Auch im Ergänzungsdreieck zeichnen wir das auf der Hypotenuse sitzende Quadrat.

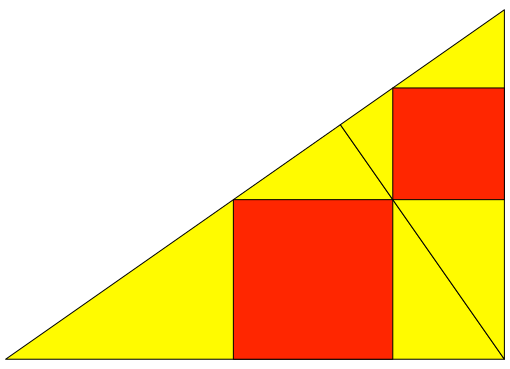
Abb. 3: Ergänzung

Wir sehen, dass die beiden Quadrate eine Ecke gemeinsam haben. Nachweis durch Rechnung. Dies ist die Thematik der Aufgabe 62 – 741 von Thomas Jahre.

2.3 Noch ein Dreieck

Nichts hindert uns, mit dem Ergänzungsdreieck gleich zu verfahren wie mit dem Startdreieck (Abb. 4). Also ein Ergänzungsdreieck des Ergänzungsdreiecks.

Abb. 4: Noch ein Dreieck

Wir können auch noch ein viertes Dreieck anhängen (Abb. 5).

Abb. 5: Viertes Dreieck

Beim fünften Dreieck fängt die Überlappung an (Abb. 6).

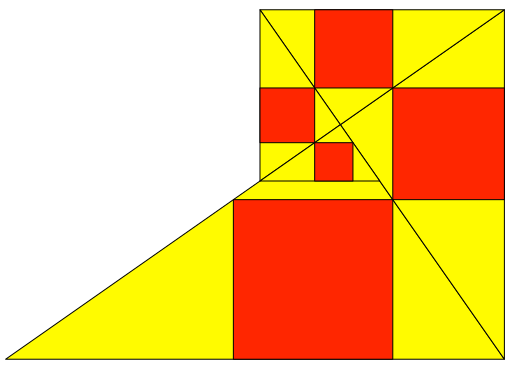
Abb. 6: Überlappung

2.4 Spirale

Die geneigte Leserin hat schon lange bemerkt, dass dies auf eine Spirale hinausläuft (Abb. 7 und 8). Es handelt sich um eine eckige logarithmische Spirale.

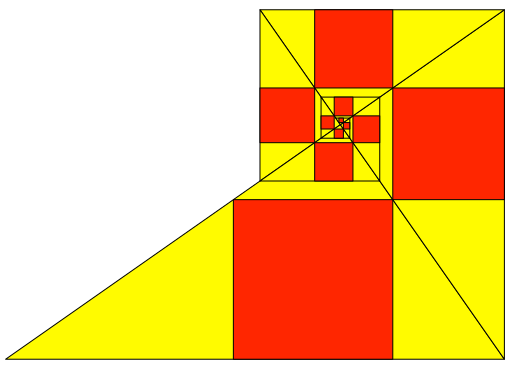
Abb. 7: Spirale

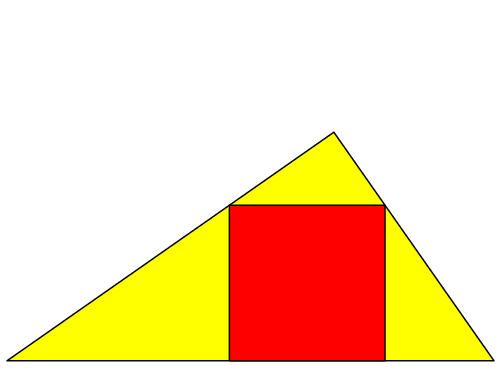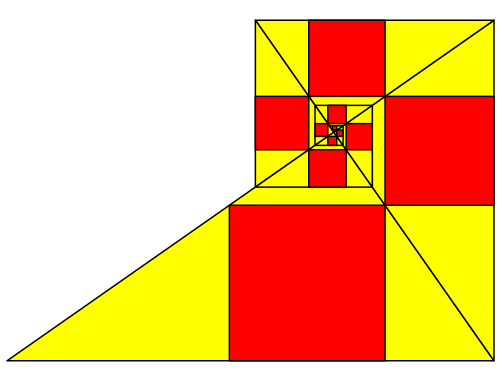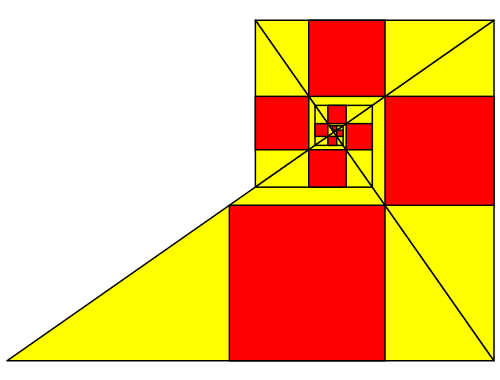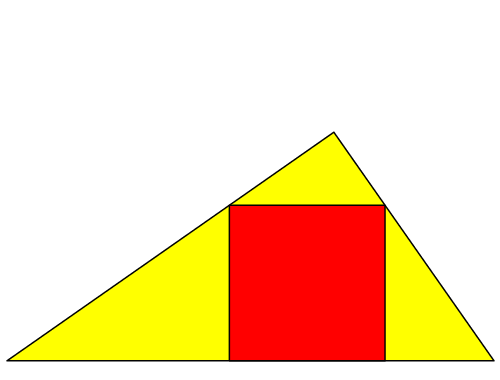
Abb. 8: Spirale

3 Variation des Startdreiecks

Bei einem variierten Startdreieck ergibt sich eine entsprechend variierte Spirale (Abb. 9 und 10).

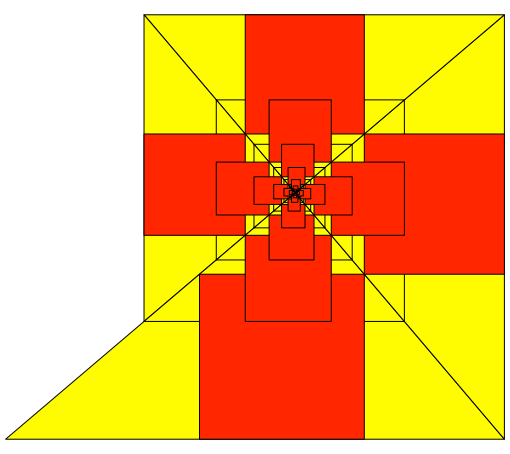
Abb. 9: Anderes Startdreieck

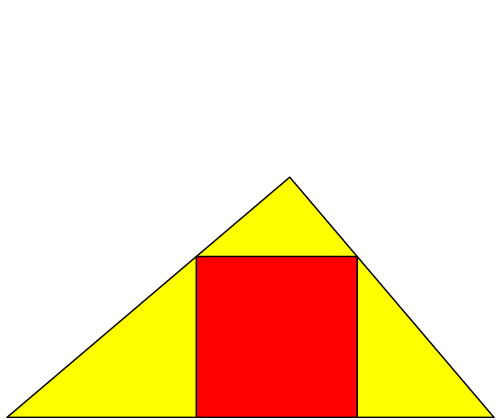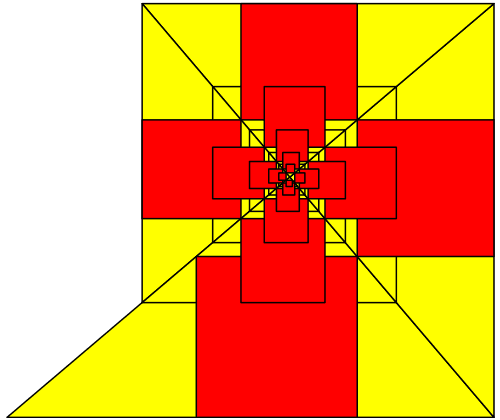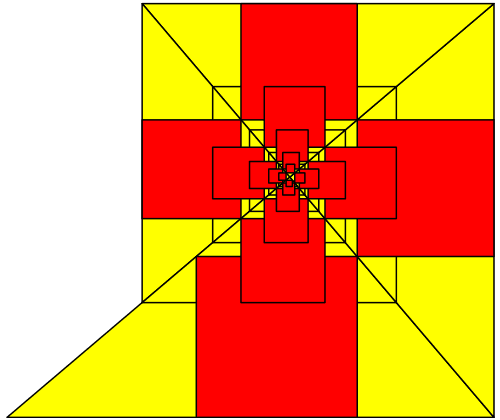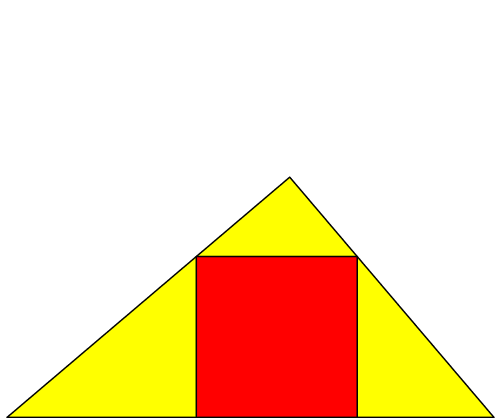
Abb. 10: Anderes Startdreieck

Bei einem rechtwinklig gleichschenkligen Dreieck gibt es gar keine Spirale (Abb. 11 und 12).

Abb. 11: Rechtwinklig gleichschenkliges Startdreieck

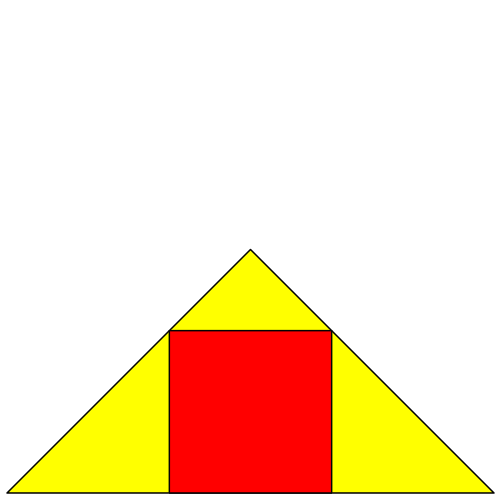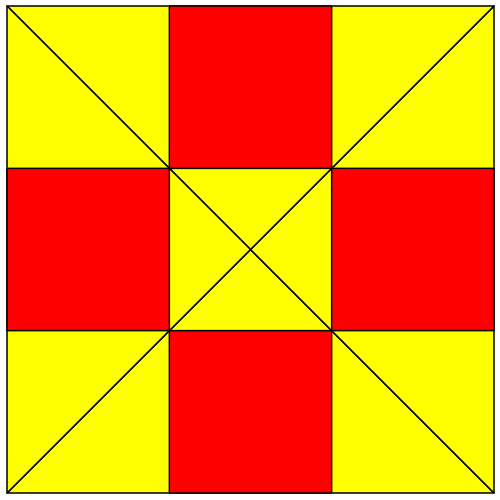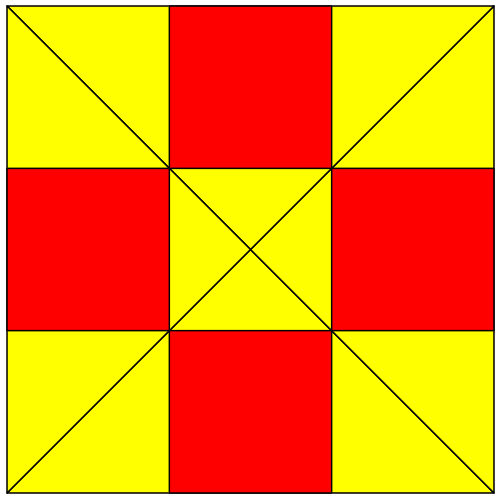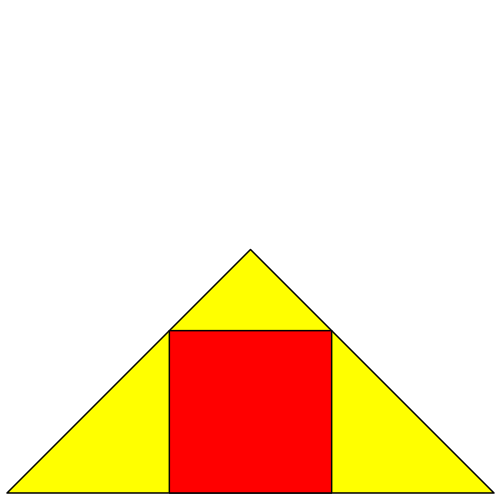
Abb.12: Rechtwinklig gleichschenkliges Startdreieck

Die Abbildung 13 zeigt eine kinematische Variation des Startdreiecks. Die Position des rechten Winkels des Startdreieckes und damit das Spiralenzentrum bleibt bei der Kinematik an Ort. Dies kann mit dem Mauszeiger überprüft werden.

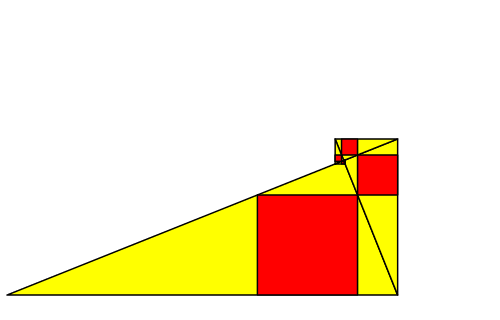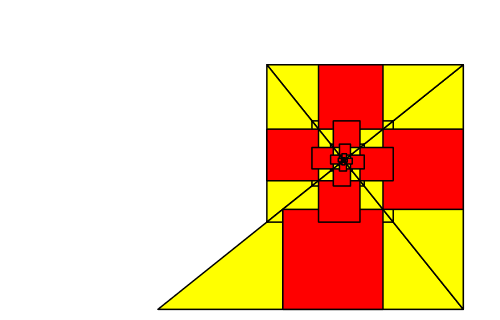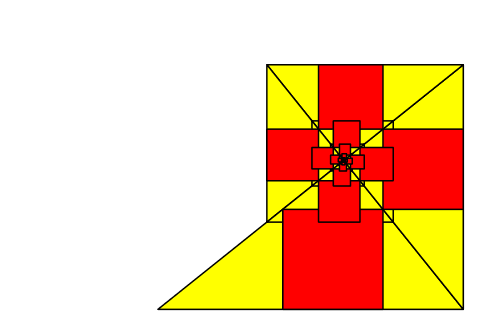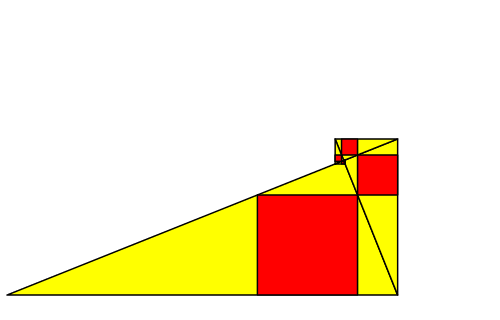
Abb. 13: Variation des Startdreiecks

4 Sonderfall

Die Abbildungen 14 und 15 zeigen einen Sonderfall. Das fünfte Quadrat sitzt genau auf dem ersten, und allgemein sitzt jedes Quadrat genau auf dem Quadrat vier Generationen vorher.

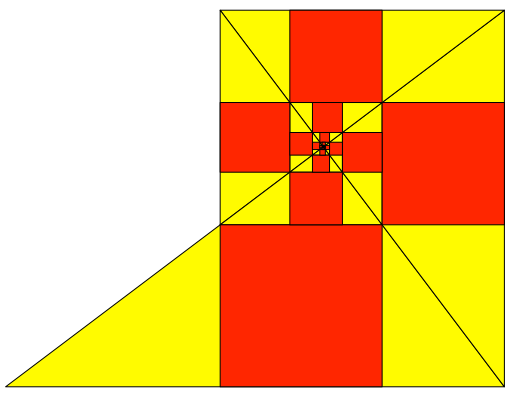
Abb. 14: Sonderfall

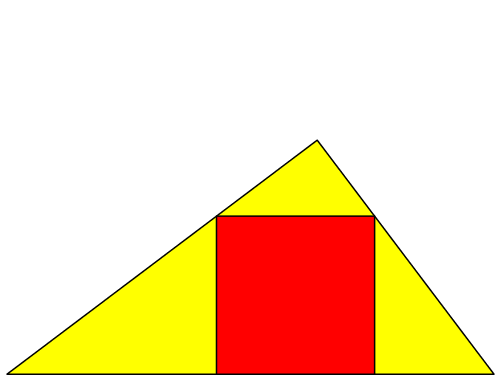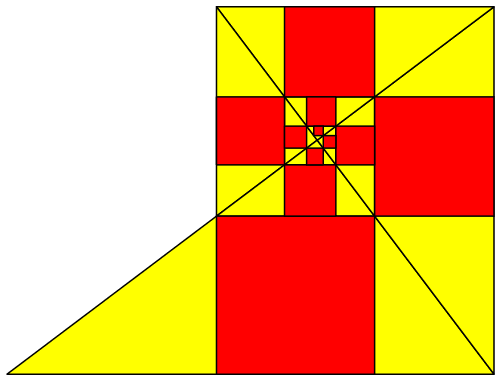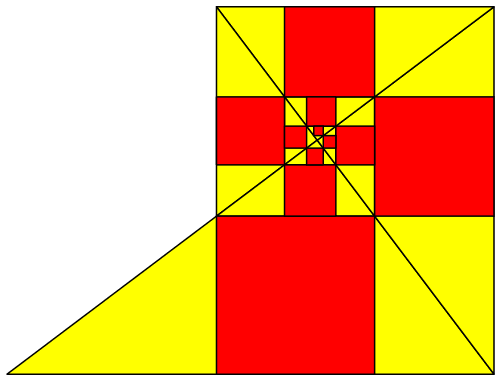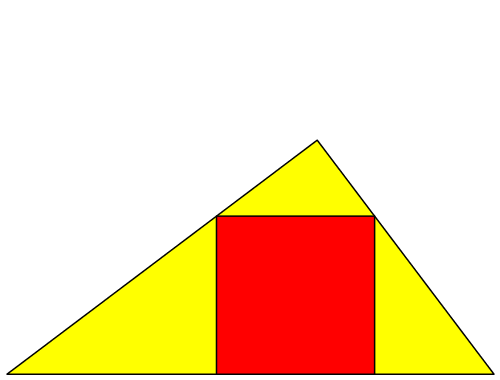
Abb. 15: Sonderfall

Etwas Rechnung: Wir bezeichnen mit f das Kathetenverhältnis (kurze Kathete zu lange Kathete) des Startdreiecks. Der Faktor f ist dann auch das Streckverhältnis von einem rechtwinkligen Dreieck zum nachfolgenden. Daher gelten die Beziehungen der Abbildung 16.

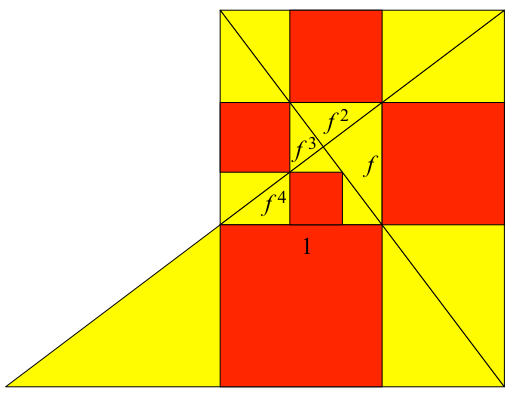
Abb. 16: Streckfaktor

Für unseren Sonderfall lesen wir die Bedingung ab:

f = f ³ + f ⁴

Wegen f ≠ 0 können wir vereinfachen zu:

f ³ + f ² – 1 = 0

Diese kubische Gleichung hat die reelle Lösung:

Dies ist ein irrationales Verhältnis, das Startdreieck ist also kein pythagoreisches Dreieck. (Für f = 0.75 hätten wir das „Lehrerdreieck“ mit dem Seitenverhältnis 3:4:5.)

Weblinks

Thomas Jahre, Aufgabe der Woche

https://www.schulmodell.eu/aufgabe-der-woche.html

Hans Walser: Quadratspirale

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadratspirale2/Quadratspirale2.html

Hans Walser: Sechseckspirale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sechseckspirale2/Sechseckspirale2.html

Hans Walser: Sechseckspirale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sechseckspirale/Sechseckspirale.html

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).