Hans Walser, [20210213]

1 Problemstellung

Die Frage, ob sich aus drei Seitenlänge a, b, c ein (reelles) Dreieck konstruieren lässt, wird durch die so genannte Dreiecksungleichung beantwortet. In Worten lautet sie so: die Summe zweier Dreiecksseiten muss größer oder gleich der dritten Seite sein. Im Falle der Gleichheit haben wir ein „flaches“ Dreieck mit dem Flächeninhalt null.

In Formeln:

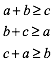(1)

Wir haben es also mit drei Ungleichungen zu tun.

Frage: Lässt sich (1) in eine einzige Ungleichung packen?

2 Bearbeitung mit dem Kosinussatz

Falls es ein reelles Dreieck gibt, lässt sich der Winkel mit dem Kosinussatz berechnen:

(2)

Für eine reelle Lösung muss:

(3)

Das sind immer noch zwei Ungleichungen. Zudem ist die Formel „unschön“, weil asymmetrisch bezüglich der drei Dreiecksseiten.

Durch Quadrieren erhalten wir:

(4)

Dies kann umgeformt werden zu:

(5)

Die Ungleichung (5) ist eine Lösung unseres Problems.

3 Mit Zirkel und Lineal

In einem kartesischen Koordinatensystem setzen wir und (Abb. 1). Die Ecke C finden wir als Schnittpunkt der beiden Kreise:

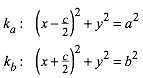(6)

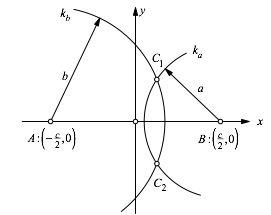
Abb. 1: Mit Zirkel und Lineal

Aus (6) erhalten wir zunächst:

(7)

Das ist immer reell. Wir setzen nun (7) in die obere Gleichung von (6) ein und erhalten:

(8)

Wir formen (8) um zu:

(9)

Für reelle Lösungen für y darf die rechte Seite von (9) nicht negativ sein. Dies ist äquivalent zu:

(10)

Die Formel (10) ist gleichwertig zur Formel (5).

4 Heronsche Formel

Mit

(11)

kann der Flächeninhalt A_Dreieck des Dreiecks nach der Heronschen Formel

(12)

berechnet werden. Für eine reelle Lösung darf der Radikand in (12) nicht negativ sein. Einsetzen von (11) in diesen Radikanden liefert:

(13)

Die Formel (13) ist äquivalent zu (5) und (10).