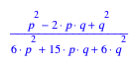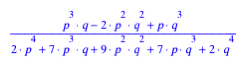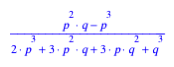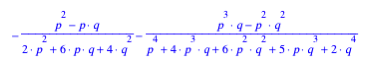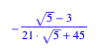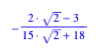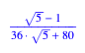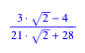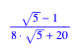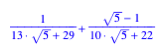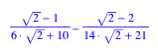Hans Walser, [20100715a]

Dreiecksunterteilung

Anregung: I. L., B.

1 Worum geht es?

Wir unterteilen die drei Seiten eines Dreieckes in den Verhältnissen und , zeichnen die sechs zugehörigen Ecktransversalen und untersuchen die dadurch entstehenden Teilgebiete des Dreieckes.

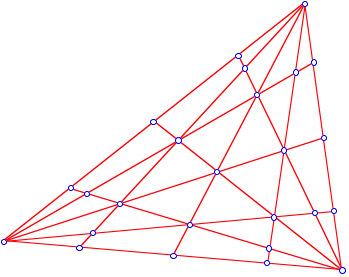
Unterteilung

2 Affine Invarianz

Für Fragen der Inzidenz (Kollinearität dreier Punkte und Kopunktalität dreier Geraden) sowie Teilverhältnisse auf einer Geraden und Flächenanteile von Polygonen können wir ausnützen, dass jedes Dreieck affin regulär ist, das heißt durch eine affine Abbildung auf ein regelmäßiges Dreieck abgebildet werden kann. Wir können also die entsprechenden Fragen beim regelmäßigen Dreieck untersuchen.

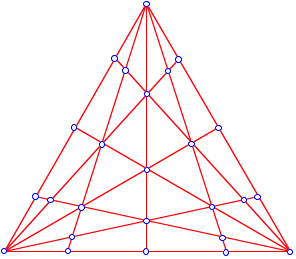
Regulärer Fall

3 Baryzentrische Koordinaten

Wir arbeiten im Folgenden mit baryzentrischen Koordinaten mit der Festlegung , und für die Dreiecksecken. Damit erhalten wir:

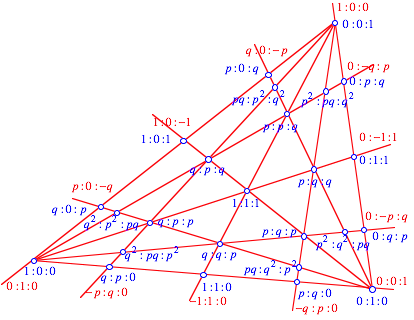
Baryzentrische Koordinaten, unnormiert

Blaue Koordinaten beziehen sich auf Punkte, rote Koordinaten auf Geraden. Die Koordinaten sind noch nicht normiert.

Wir können aber schon mal zeigen, dass die sechs Punkte , , , , und jeweils auf Seitenhalbierenden liegen. Es ist zum Beispiel:

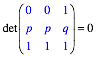und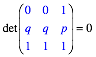

Daher sind die Punkte , , kollinear und ebenso die Punkte , , (vgl. [Kennedy 1993]). Dies folgt wegen der affinen Invarianz auch direkt aus dem regulären Fall.

4 Normierung

Um Längenverhältnisse auf einer Geraden zu berechnen, benötigen wir normierte baryzentrische Koordinaten. Wir normieren wie folgt:

Wenn wir die normierten baryzentrischen Koordinaten als kartesische 3d-Koordinaten interpretieren, erhalten wir folgende Situation:

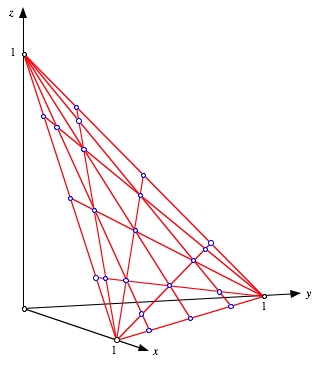
Darstellung im Raum

Die Figur liegt in der Ebne . Es wird automatisch der Fall des regulären Dreiecks dargestellt.

5 Längenverhältnisse

Aus Symmetriegründen (in der Darstellung des regulären Dreiecks) sind die Längenverhältnisse auf vielen Geraden gleich. Wir haben im Prinzip nur drei Geradentypen: Dreiecksseiten, Seitenhalbierende, Ecktransversalen

5.1 Dreiecksseiten

Wir bearbeiten die Dreiecksseite .

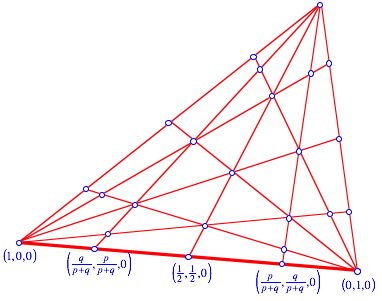
Dreiecksseite

Damit erhalten wir aber nur die Daten der Aufgabe.

5.2 Seitenhalbierende

Wir bearbeiten die Seitenhalbierende .

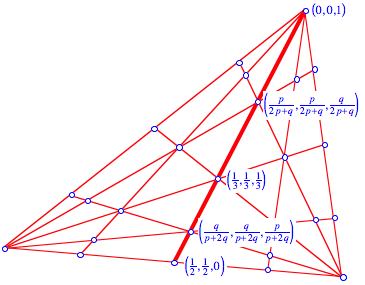
Seitenhalbierende

Wir sehen anhand der jeweiligen dritten Koordinaten (welche aufwärts von 0 bis 1 läuft), dass der untere Ecktransversalen-Schnittpunkt auf dem relativen Niveau , der Schwerpunkt auf dem relativen Niveau und der obere Ecktransversalen-Schnittpunkt auf dem relativen Niveau liegt. Für den Niveau-Unterschied der beiden Ecktransversalen-Schnittpunkte ergibt sich:

Das kann auch so formuliert werden: Die Summe der Längen der der Mittelpunktsdiagonalen des gelb markierten Sechseckes ist gleich mal die Summe der Seitenhalbierendenlängen.

Sechseck in der Mitte

Zahlenbeispiele:

Für , , das heißt beim Dritteln der Dreiecksseiten ist der untere Ecktransversalen-Schnittpunkt auf dem Niveau und der obere Ecktransversalen-Schnittpunkt auf dem Niveau (also auf der Mittelparallel des Dreiecks). Niveau-Unterschied .

Für , , das heißt beim Vierteln der Dreiecksseiten ist der untere Ecktransversalen-Schnittpunkt auf dem Niveau und der obere Ecktransversalen-Schnittpunkt auf dem Niveau . Niveau-Unterschied .

5.3 Ecktransversalen

Wir bearbeiten die Ecktransversale .

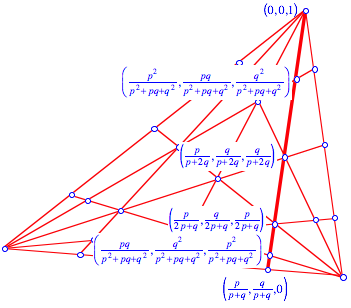
Ecktransversale

Für die Punkte haben wir von unten nach oben die relativen Niveaus (dritte Koordinate):

Für die auf dieser Ecktransversalen liegende Seite des oben gelb markierten erhalten wir die Niveaudifferenz:

Somit ist der Umfang dieses Sechseckes gleich mal die Summe der Längen aller sechs Ecktransversalen.

Der Faktor ist halb so groß wie der Faktor , den wir bei den Längen der Mittelpunktsdiagonalen angetroffen haben. Es ist aber zu beachten, dass diese Faktoren sich auf unterschiedlich lange Strecken beziehen.

6 Flächenanteile

Wenn wir den Flächeninhalt des Basisdreieckes auf 1 normieren, kann der Flächenanteil eines Dreiecks DEF mit den normierten baryzentrischen Eckpunktskoordinaten , , mit der Determinante

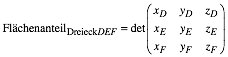
berechnet werden. Um das einzusehen, denken wir uns in der Darstellung im Raum eine Pyramide über dem Dreieck DEF mit der Spitze im Ursprung des räumlichen Koordinatensystems. Da alle solche Pyramiden, einschließlich der Pyramide über dem Basisdreieck, dieselbe Höhe haben, entsprechen die Volumenverhältnisse den Grundflächenverhältnissen.

Im regulären Dreieck sehen wir, dass jeder Flächenanteil sechs Mal erscheint.

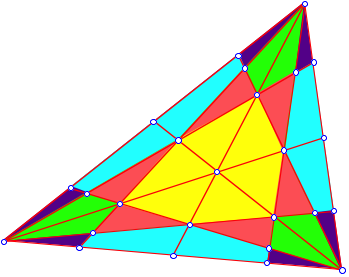
Flächenunterteilung

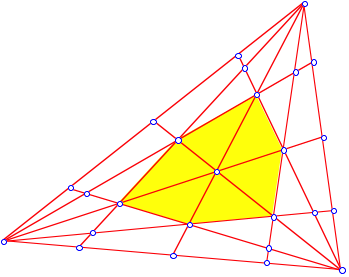
6.1 Gelbes Dreieck

Das gelbe Dreieck rechts unten hat die Eckpunktskoordinaten , und . Für seinen Flächenanteil erhalten wir:

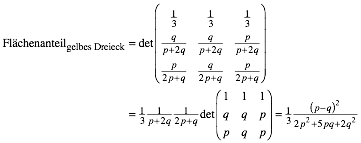
6.2 Übersicht

Analog können wir die übrigen Flächenanteile berechnen. Wir erhalten:

Gelbes Dreieck
Rotes Dreieck
Grünes Dreieck
Hellblaues Viereck
Violettes Dreieck
Summe

6.3 Beispiele

6.3.1 Rationale Teilverhältnisse

Farbe \ p und q
Stichwort	Dritteln	Vierteln	Fünfteln 1	Fünfteln 2	Siebteln 2
Gelbes Dreieck
Rotes Dreieck
Grünes Dreieck
Hellblaues Viereck
Violettes Dreieck
Summe

Bei (Fünfteln) bedeckt das gelbe Sechseck einen Drittel der Dreiecksfläche.

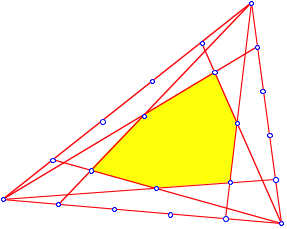
Ein Drittel ist gelb

Bei (Siebteln) bedeckt das gelbe Sechseck einen Sechstel der Dreiecksfläche.

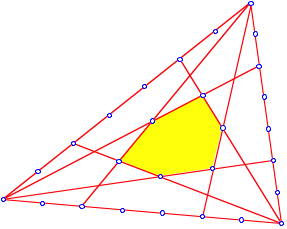
Ein Sechstel ist gelb

6.3.2 Goldener Schnitt und DIN-Format

Farbe \ p und q
Stichwort	Goldener Schnitt	DIN-Format
Gelbes Dreieck
Rotes Dreieck
Grünes Dreieck
Hellblaues Viereck
Violettes Dreieck
Summe

6.3.3 Weitere irrationale Teilverhältnisse

Wir wollen erreichen, dass das gelbe zentrale Sechseck einen vorgegebenen Flächenanteil des Dreiecks hat, zum Beispiel die Hälfte. Mit der Normierung erhalten wir dafür die Bedingung:

Farbe \ p und q
Sechsecksgröße	Halbes Dreieck
Gelbes Dreieck
Rotes Dreieck
Grünes Dreieck
Hellblaues Viereck
Violettes Dreieck
Summe

Im folgenden Beispiel soll das gelbe zentrale Sechseck einen Viertel der Dreiecksfläche ausmachen.

Farbe \ p und q
Sechsecksgröße	Viertel des Dreieckes
Gelbes Dreieck
Rotes Dreieck
Grünes Dreieck
Hellblaues Viereck
Violettes Dreieck
Summe

Literatur

[Kennedy 1993] Kennedy, Joe: (Responds to) Marion’s Theorem. Math. Teacher 86, 1993, p. 619