Hans Walser, [20170902]
Dreiecksunterteilung mit Seitenhalbierenden
Anregung: Hlzl 2017
1 Worum geht es?
Wir unterteilen ein Dreieck mit einer Seitenhalbierenden und iterieren den Prozess.
2 Unterteilungsmglichkeiten
Wir zeichnen nur eine Seitenhalbierende ein (Abb. 1). Die Teildreiecke haben unterschiedliche Form, aber den gleichen Flcheninhalt.
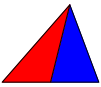
Abb. 1: Unterteilung mit Seitenhalbierender
Fr den zweiten Unterteilungsschritt gibt es mehrere Mglichkeiten.
2.1 Fcher
Wir zeichnen bei den beiden nachfolgenden Unterteilungen die Seitenhalbierenden von derselben Ecke aus wie bei der vorangehenden Unterteilung. Es entsteht ein Fcher (Abb. 2). Bisschen langweilig.
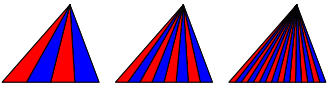
Abb. 2: Fcher
2.2 Raster
Bei den nachfolgenden Unterteilungen zeichnen wir die Seitenhalbierenden von der Seitenmitte der vorangehenden Unterteilung aus. Es entsteht ein Dreiecksraster (Abb. 3). Nicht sonderlich interessant.
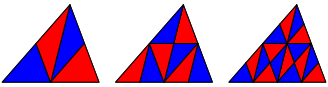
Abb. 3: Raster
2.3 Gegenpunkt
Bei den nachfolgenden Unterteilungen zeichnen wir die Seitenhalbierenden vom Gegenpunkt der vorangehenden Unterteilungsseitenhalbierenden aus (Abb. 4).
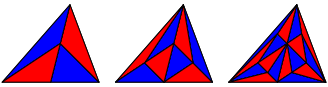
Abb. 4: Etwas Neues
Das sieht nun interessanter aus.
Die Abbildung 5 zeigt die siebte Unterteilung nach diesem Verfahren.

Abb. 5: Siebte Unterteilung
2.4 Kombinationen
2.4.1 Fcher und Raster
Wir kombinieren Fcher und Raster (Abb. 6). Es entstehen innere Teilpunkte, an denen drei Teildreiecke zusammenkommen. Wir bruchten mehr als zwei Farben, um das wie eine Landkarte zu kolorieren.
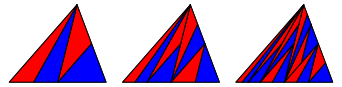
Abb. 6: Fcher und Raster
2.4.2 Fcher und Gegenpunkt
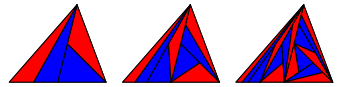
Abb. 7: Fcher und Gegenpunkt
Auch hier kommen wir nicht mehr mit zwei Farben aus.
2.4.3 Raster und Gegenpunkt
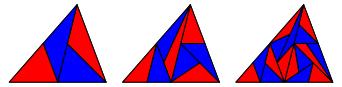
Abb. 8: Raster und Gegenpunkt
3 Gleichseitiges Dreieck
Das Unterteilen mit Seitenhalbierenden ist affin invariant. Wir knnen also die bisherigen Unterteilungen auf ein gleichseitiges Dreieck affin abbilden.
Die Abbildung 9 zeigt die siebte Unterteilung (vgl. Abb. 5) fr ein gleichseitiges Dreieck.

Abb. 9: Gleichseitiges Dreieck
Die Figur hat nicht die dreiteilige Rotationssymmetrie wie das gleichseitige Dreieck. Das liegt daran, dass durch die erste Seitenhalbierende die Rotationssymmetrie zerstrt wird.
Wir knnen sechs Exemplare der Abbildung 9 zu einem Sechseck zusammenfgen (Abb. 10).

Abb. 10: Sechseck
In der Abbildung 11 ist aus einer vereinfachten Version (nur 5 Unterteilungen) ein Bienenwabenmuster gelegt.

Abb. 11: Bienenwabenmuster
In [1] wird die iterierte Unterteilung eines rechtwinkligen Dreiecks durch die Hhe besprochen.
Literatur
Hlzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und Zusammenhnge findest du? mathematik lehren 201 | 2017, 12-15.
Websites
[1] Hans Walser: Dreiecksunterteilung und Binomialverteilung (abgerufen 3.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung2/Dreiecksunterteilung2.htm