Hans Walser, [20170903]
Dreiecksunterteilung mit Winkelhalbierenden
Anregung: Hšlzl 2017
1 Worum geht es?
Wir unterteilen ein Dreieck mit einer Winkelhalbierenden und iterieren den Prozess.
2 Unterteilungsmšglichkeiten
Wir zeichnen nur eine Winkelhalbierende ein (Abb. 1).
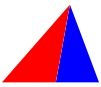
Abb. 1: Unterteilung mit Winkelhalbierender
FŸr den zweiten Unterteilungsschritt gibt es mehrere Mšglichkeiten.
2.1 FŠcher
Wir zeichnen bei den beiden nachfolgenden Unterteilungen die Winkelhalbierenden von derselben Ecke aus wie bei der vorangehenden Unterteilung. Es entsteht ein FŠcher (Abb. 2). Bisschen langweilig.
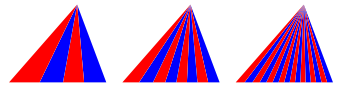
Abb. 2: FŠcher
2.2 Fu§punkt
Bei den nachfolgenden Unterteilungen zeichnen wir die Winkelhalbierenden vom Winkelhalbierendenfu§punkt der vorangehenden Unterteilung aus (Abb. 3).
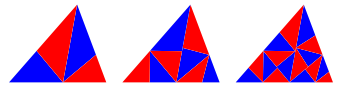
Abb. 3: Fu§punktlšsung
Wir sehen, dass die Farbabgrenzung nicht mehr spielt. Wir mŸssten mit weiteren Farben arbeiten.
2.3 Gegenpunkt
Bei den nachfolgenden Unterteilungen zeichnen wir die Winkelhalbierenden vom Gegenpunkt der vorangehenden Unterteilungswinkelhalbierenden aus (Abb. 4).
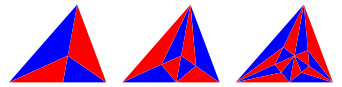
Abb. 4: Gegenpunkt
Das sieht nun interessanter aus.
Die Abbildung 5 zeigt die siebte Unterteilung nach diesem Verfahren.
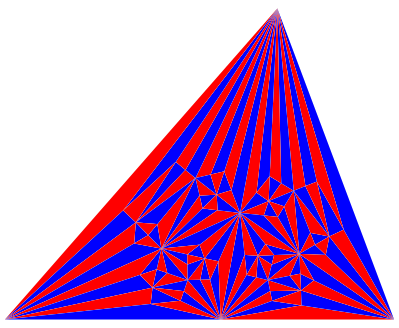
Abb. 5: Siebte Unterteilung
3 Gleichseitiges Dreieck
Die Abbildung 6 zeigt die siebte Unterteilung (vgl. Abb. 5) fŸr ein gleichseitiges Dreieck.
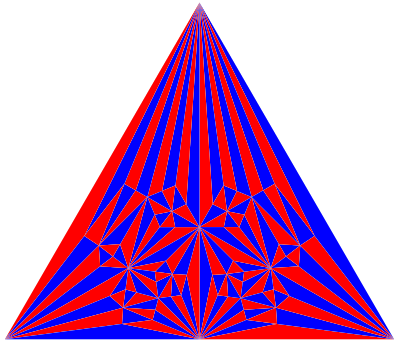
Abb. 6: Gleichseitiges Dreieck
Die Figur hat nicht die dreiteilige Rotationssymmetrie wie das gleichseitige Dreieck. Das liegt daran, dass durch die erste Winkelhalbierende die Rotationssymmetrie zerstšrt wird.
Wir kšnnen sechs Exemplare der Abbildung 6 zu einem Sechseck zusammenfŸgen (Abb. 7).
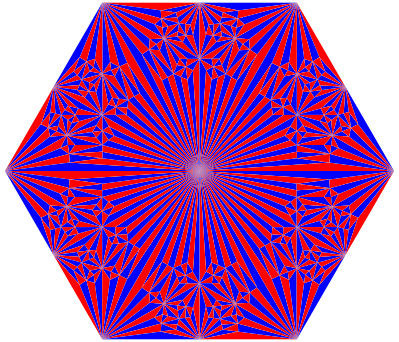
Abb. 7: Sechseck
In der Abbildung 8 ist aus einer vereinfachten Version (nur 5 Unterteilungen) ein Bienenwabenmuster gelegt.

Abb. 8: Bienenwabenmuster
In [1] wird die iterierte Unterteilung eines rechtwinkligen Dreiecks durch die Hšhe besprochen.
In [2] wird die iterierte Unterteilung eines Dreieckes durch eine Seitenhalbierende besprochen.
Literatur
Hšlzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und ZusammenhŠnge findest du? mathematik lehren 201 | 2017, 12-15.
Websites
[1] Hans Walser: Dreiecksunterteilung und Binomialverteilung (abgerufen 3.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung2/Dreiecksunterteilung2.htm
[2] Hans Walser: Dreiecksunterteilung mit Seitenhalbierenden (abgerufen 3.9.2017):
www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung3/Dreiecksunterteilung3.htm