Hans Walser, [20200132]

Dritte binomische Formel

1 Worum geht es?

Mit der dritten binomischen Formel p² – q² = (p + q)(p – q) kann ein Verfahren der Quadratur des Rechteckes bewiesen werden.

2 Das Verfahren

Die Figurenfolge 1 zeigt das Verfahren.

Abb. 1.1: Rechteck

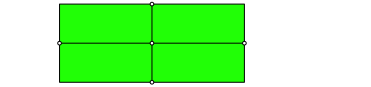
Abb. 1.2: Vierteln

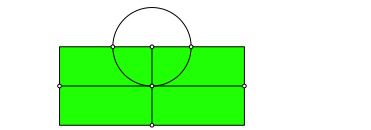
Abb.1.3: Kreis

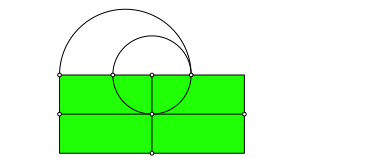
Abb. 1.4: Thaleskreis

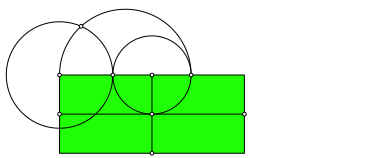
Abb. 1.5: Noch ein Kreis

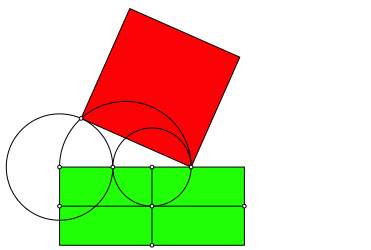
Abb. 1.6: Flächengleiches Quadrat

3 Der Beweis

Wir verwenden die Bezeichnungen der Abbildung 2.

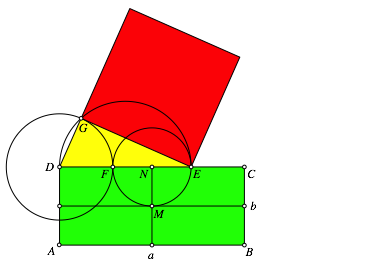
Abb. 2: Bezeichnungen

Das Rechteck ABCD hat den Flächeninhalt ab. Weiter ist:

(1)

Dies sind die Hypotenuse und die eine Kathete des gelb eingezeichneten rechtwinkligen Dreiecks DEG. Nach dem Satz des Pythagoras hat das rote Kathetenquadrat daher den Flächeninhalt S:

(2)

Gemäß der dritten binomischen Formel ergibt sich:

(3)

Dies war zu zeigen.

4 Vergleich

Die Abbildung 3 zeigt den Vergleich mit den Konstruktionen mit dem Höhensatz (magenta) und dem Kathetensatz (orange).

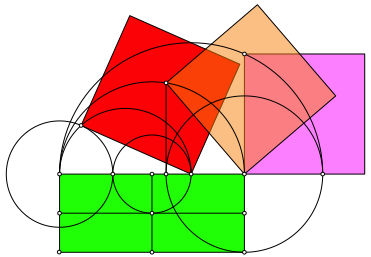
Abb. 3: Vergleich