Hans Walser, [20101114c]
Dritteln der Dreiecksseiten
Anregung: I. L., B.
1 Worum geht es?
Wir
dritteln zyklisch die drei Seiten eines Dreiecks ![]() . Den ersten Drittelspunkt auf der Seite
. Den ersten Drittelspunkt auf der Seite ![]() (zyklische
Indizierung) sei
(zyklische
Indizierung) sei ![]() (Abbildung).
Weiter sei
(Abbildung).
Weiter sei ![]() der Schnittpunkt
der beiden Ecktransversalen
der Schnittpunkt
der beiden Ecktransversalen ![]() und
und ![]() .
.
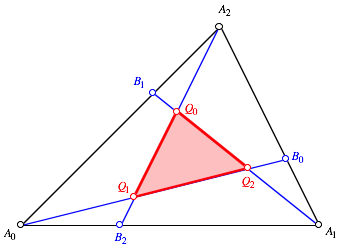
Dritteln der Dreiecksseiten
Dann gilt ([Johnston 1992], [Sielaff/ Usbeck 1994], [Steinhaus 1959]):
Das
Dreieck ![]() bedeckt flchenm§ig einen Siebtel der
Dreiecksflche
bedeckt flchenm§ig einen Siebtel der
Dreiecksflche ![]() .
.
2 Beweise
2.1 Rasterung
Die
Situation passt in ein Dreiecksraster mit 49 kongruenten, zum Ausgangsdreieck ![]() hnlichen
Dreiecken (Abbildung).
hnlichen
Dreiecken (Abbildung).
Dass die Sache mit der Drittelung der Dreiecksseiten stimmt, sehen wir exemplarisch an der grn eingezeichneten Referenzzeile.
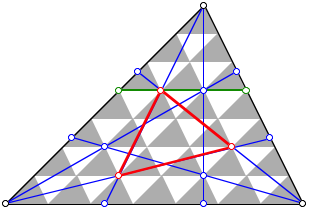
Rasterung
Aus diesem Raster knnen wir die Teilverhltnisse auf den Ecktransversalen ablesen.
Wir sehen
auch noch ein ãspiegelbildlichesÒ (Schrgspiegelung an Seitenhalbierenden)
Dreieck, das natrlich denselben Flcheninhalt hat wie das rote Dreieck ![]() .
.
2.2 ãKleinerÒ Zerlegungsbeweis
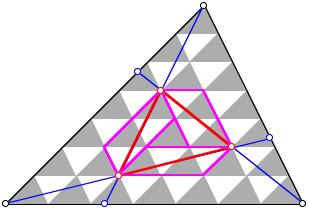
ãKleinerÒ Zerlegungsbeweis
Wir
arbeiten mit den Dreiecken des Rasters als Ma§einheit. Diese messen je ![]() der Flche des
Ausgangsdreiecks
der Flche des
Ausgangsdreiecks ![]() . In der Abbildung sind drei magenta Parallelogramme
eingezeichnet, welche je vier Rasterdreiecke umfassen. Flchenm§ig liegt
jeweils genau die Hlfte dieser Parallelogramme im Innern des roten Dreiecks
. In der Abbildung sind drei magenta Parallelogramme
eingezeichnet, welche je vier Rasterdreiecke umfassen. Flchenm§ig liegt
jeweils genau die Hlfte dieser Parallelogramme im Innern des roten Dreiecks ![]() . Zustzlich haben wir in der Mitte des roten Dreiecks
. Zustzlich haben wir in der Mitte des roten Dreiecks ![]() noch ein
einzelnes Rasterdreieck. Fr die Flche des roten Dreiecks
noch ein
einzelnes Rasterdreieck. Fr die Flche des roten Dreiecks ![]() erhalten wir
somit
erhalten wir
somit ![]() Rasterdreiecke,
also eine Siebtel des Ausgangsdreiecks
Rasterdreiecke,
also eine Siebtel des Ausgangsdreiecks ![]() .
.
2.3 ãGro§erÒ Zerlegungsbeweis
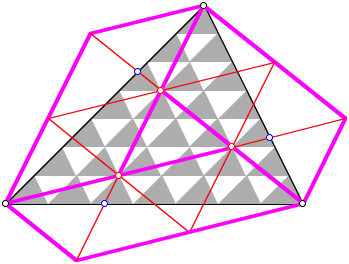
ãGro§erÒ Zerlegungsbeweis
Wir
expandieren das rote Dreieck ![]() zu einem Raster.
Das ursprngliche Dreieck
zu einem Raster.
Das ursprngliche Dreieck ![]() passt in dieses
gro§e Raster. Das gro§e Raster enthlt drei magenta Parallelogramme aus je vier
Rasterdreiecken, welche je zur Hlfte das Ausgangsdreieck
passt in dieses
gro§e Raster. Das gro§e Raster enthlt drei magenta Parallelogramme aus je vier
Rasterdreiecken, welche je zur Hlfte das Ausgangsdreieck ![]() bedecken.
Zustzlich haben wir im Innern das ursprngliche Rasterdreieck
bedecken.
Zustzlich haben wir im Innern das ursprngliche Rasterdreieck ![]() . Das Ausgangsdreieck
. Das Ausgangsdreieck ![]() besteht also flchenm§ig
aus
besteht also flchenm§ig
aus ![]() Rasterdreiecken.
Rasterdreiecken.
Literatur
[Johnston 1992] Johnston, W. I.: Mathematics Teacher 85(2), 1992, Titelbild sowie S. 89, 92, 598.
[Sielaff/ Usbeck 1994] Sielaff, K. / Usbeck, F. W.: Hamburger Schlerzirkel Mathematik 1991-93. Hamburg, Hereus, 1994. S. 176-177.
[Steinhaus 1959] Steinhaus, H.: Kaleidoskop der Mathematik. Berlin: DVW,1959. S. 17.