Hans Walser, [20111218a]

Dritteln im DIN-Format

Durch Falten erhalten wir aus einem Blatt im DIN-A4-Format ein Rechteck, dessen SeitenlŠngen gegenŸber dem DIN-A4-Rechteck gedrittelt sind.

1        Faltprozess

Wir falten in einem DIN-A4-Blatt (Querformat, Abb. 1) die Mittelsenkrechte zweier diametralen Ecken.

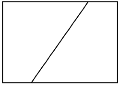
Abb. 1: Erster Schritt: Mittelsenkrechte

Nun falten wir die gelb markierten rechtwinkligen Dreiecke an ihrer Hypotenuse hinein (Abb. 2). Das entstehende Umrissviereck ist ein Rhombus.

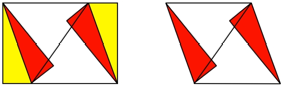
Abb. 2: Zweiter Schritt: Hineinfalten zweier Dreiecke. Umrissrhombus

Anschlie§end falten wir die beiden cyan markierten rechtwinkligen Dreiecke (sie sind kongruent zu den gelb markierten Dreiecken im zweiten Faltschritt) an der langen Kathete hinein (Abb. 3). Das Umrissviereck ist ein Rechteck, ebenso das restliche ãLochviereckÒ.

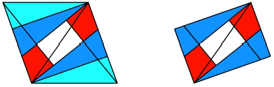
Abb. 3: Dritter Schritt: Hineinfalten zweier Dreiecke. Umrissrechteck und Lochrechteck

Nun gilt:

á    Das Umrissrechteck hat das DIN-A5-Format.

á    Das Lochrechteck ist gegenŸber dem ursprŸnglichen DIN-A4-Rechteck lŠngenmŠ§ig auf einen Drittel verkleinert. (Es ist etwas kleiner als das DIN-A7-Rechteck).

2        Beweis

Wir bezeichnen im gelben rechtwinkligen Dreieck die Katheten mit a und b und die Hypotenuse mit c. Weiter verwenden wir die Bezeichnungen der Abbildung 4.

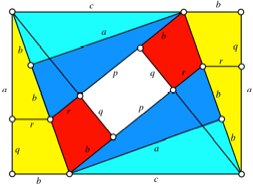
Abb. 4: Bezeichnungen

ZunŠchst ist .

Das Ausgangsrechteck hat das SeitenverhŠltnis , das Umrissrechteck nach dem Faltprozedere das SeitenverhŠltnis . Wegen  sind diese beiden SeitenverhŠltnisse gleich. Das Umrissrechteck nach dem Faltprozedere ist also in jedem Fall Šhnlich zum Ausgangsrechteck, unabhŠngig davon, ob es sich um ein DIN-Format handelt oder nicht.

Aus dem DIN-Format des Ausgangsrechtecks folgt weiter:

Es ist also . Eingesetzt in die Formel von Pythagoras erhalten wir:

Damit ist . Es ist also . Hier erscheint zum ersten Mal die Zahl 3. Die Hypotenuse c wird durch die kurze Kathete b gedrittelt.

Das Umrissrechteck nach dem zweiten Faltschritt hat die LŠnge a und die Breite

.

Dieses Umrissrechteck hat also das DIN-A5-Format.

Wir berechnen nun weiter die Hilfsgrš§e r. Aus dem Strahlensatz im rechtwinkligen Dreieck folgt:

Damit ist:

Weiter ist:

Zusammengefasst:

Das Lochrechteck ist gegenŸber dem ursprŸnglichen DIN-A4-Rechteck lŠngenmŠ§ig auf einen Drittel verkleinert.

Auch das Lochrechteck ist, unabhŠngig vom DIN-Format, Šhnlich zum Ausgangsrechteck. Dies kann wie folgt nachgerechnet werden. FŸr die Hilfsgrš§e r erhalten wir unabhŠngig vom DIN-Format, die Beziehung , also .

Damit erhalten wir:

Weiter ist:

Zu prŸfen ist:

Also:

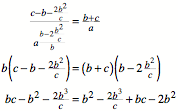
Die Gleichheit ist erfŸllt.

Das Spezielle am DIN-Format ist also lediglich das Auftreten des Faktors .

Die Abbildung 5 zeigt die Situation in einem nicht-DIN-Rechteck.

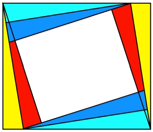
Abb. 5: Kein DIN-Rechteck

3        Variante

Wir unterteilen die Schmalseite eines DIN-Rechteckes in zwei und die LŠngsseite in vier Teile. Dann verbinden wir mit schrŠgen Linien gemŠ§ Abbildung 6.

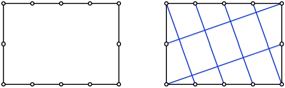
Abb. 6: Unterteilung

Die beiden Scharen von schrŠgen Linien schneiden sich orthogonal. Dies ist eine Folge des DIN-Formates. Der Beweis sei der Leserin Ÿberlassen.

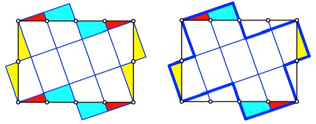
Abb. 7: Abschneiden und Ansetzen

Nun legen wir einzelne Teile um gemŠ§ Abbildung 7 und erhalten neun kongruente Rechtecke. Sie sind Šhnlich zum Ausgangsrechteck, ihre SeitenlŠngen sind daher ein Drittel der entsprechenden SeitenlŠngen des Ausgangsrechtecks.

Bei einem beliebigen Ausgangsrechteck liefert das Unterteilungsverfahren neun kongruente Parallelogramme (Abb. 8).

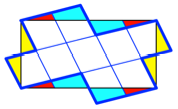
Abb. 8: Parallelogramme