Hans Walser, [20080105b]
Dualbrche
1 Problemstellung
Fr ![]() soll eine
Dualbruchdarstellung gefunden und visualisiert werden.
soll eine
Dualbruchdarstellung gefunden und visualisiert werden.
2 Pseudodualbruch
Das MuPAD Programm gibt
effektiv einen Dezimalbruch, der aber so aussieht wie das gesucht Resultat.
x:=3/5:
n:=12:
bin:=proc(x)
begin
s:=0:
for i from 1 to n do
if 2*x<1 then
s:=s: x:=2*x
else
s:=s+(1/10)^i: x:=2*x-1
end_if
end_for:
float(s);
end_proc:
print(NoNL, x):
print(Unquoted, " entspricht ".bin(x)):
3/5 entspricht 0.100110011
Die Stellenanzahl ist
beschrnkt.
3
Dualbruch
Das folgende Programm
berechnet echt die Ziffern. Die
Stellenzahl n ist unbeschrnkt.
x:=3/5:
n:=32:
x1:=x:
for i from 1 to n do
if x1<1/2 then
y[i]:=0:
x1:=2*x1:
else
y[i]:=1:
x1:=2*x1-1:
end_if:
end_for:
print(NoNL, x):
print(NoNL, " entspricht 0."):
for i from 1 to n do
print(NoNL, y[i]):
end_for:
3/5 entspricht 0.10011001100110011001100110011001
4
OL-Darstellung
Variante in der
OL_Darstellung.
x:=3/5:
n:=24:
x1:=x:
for i from 1 to n do
if x1<1/2 then
y[i]:="O":
x1:=2*x1:
else
y[i]:="L":
x1:=2*x1-1:
end_if:
end_for:
print(NoNL, x):
print(NoNL, " entspricht O."):
for i from 1 to n do
print(NoNL, y[i]):
end_for:
3/5 entspricht O.LOOLLOOLLOOLLOOLLOOLLOOL
5
Monotone Grafik
Der Wert wird von links
her angeschlichen. Jede 1 (oder jedes L) bedeutet Weg nach rechts oben, jede 0
(oder jedes O) bedeutet Weg senkrecht nach oben.
x:=3/5:
x1[0]:=0:
x0:=x:
for i from 1 to n do
if x0<1/2 then
x1[i]:=x1[i-1]:
x0:=2*x0:
else
x1[i]:=x1[i-1]+(1/2)^i:
x0:=2*x0-1:
end_if:
end_for:
start:=plot::Point2d([x,0],PointSize=4, PointColor=[0,0,1] ):
punkt:=plot::PointList2d([[x1[i],i]$i=0..n], PointSize=2,
PointColor=[1,0,0]):
pol:=plot::Polygon2d([[x1[i],i]$i=0..n], LineWidth=1/2,
LineColor=[1,0,0]):
plot(pol, punkt, start,
TicksDistance=1, TicksBetween=0,
ViewingBox=[0..1, 0..n], AxesTitles = ["x",
"i"],
Width=70, Height=70,
BorderWidth=1/4*unit::mm);
Das ergibt fr ![]() folgendes Bild:
folgendes Bild:
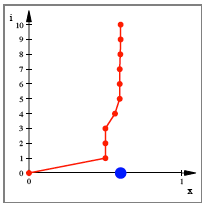
Anschleichen von links
Man kann auch die
Steigung vereinheitlichen; dann hat die ganze Grafik im Einheitsquadrat Platz.
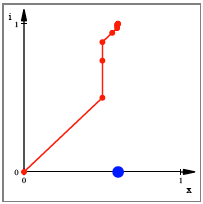
Einheitliche Steigung
6
Zickzack-Grafik
Der Wert wird
allenfalls bersprungen. Fr ![]() erhalten wir:
erhalten wir:
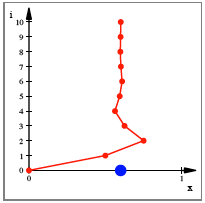
Zickzack
Auch hier kann die
Steigung vereinheitlicht werden. Wegen der Periodizitt von ![]() mit der
Periodenlnge 4 ist die Zickzacklinie selbsthnlich (Faktor
mit der
Periodenlnge 4 ist die Zickzacklinie selbsthnlich (Faktor ![]() . Auf Grund der geringen Auflsung ist das in der Figur
schlecht sichtbar.
. Auf Grund der geringen Auflsung ist das in der Figur
schlecht sichtbar.
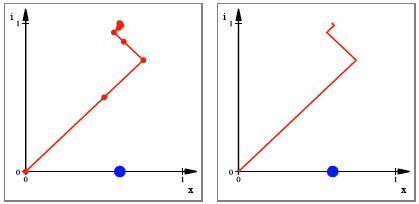
Einheitliche Steigung
Die folgende Figur
zeigt die Selbsthnlichkeit fr ![]() . Die Periodenlnge ist 2, der Faktor
. Die Periodenlnge ist 2, der Faktor ![]()
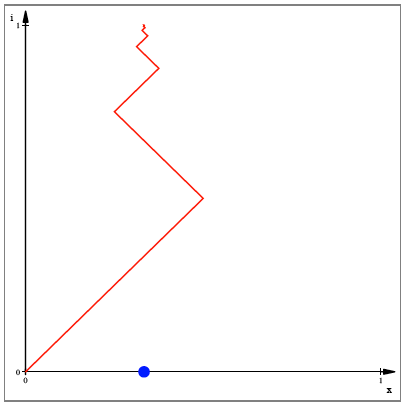
Selbsthnlichkeit
7
Mehrfachgrafiken
Fr smtliche Fnftel
ergibt sich:
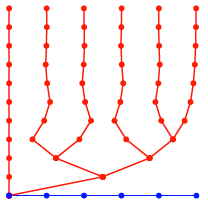
Fnftel
Fr Fnfzehntel und
Sechzehntel erhalten wir eine unregelm§ige respektive eine recht regelm§ige
Figur, weil 16 eine Potenz von 2 ist.
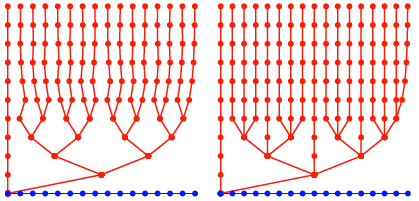
Fnfzehntel und
Sechzehntel