Hans Walser, [20120903]
DualbrŸche
1 Worum geht es?
Visualisierung der DualbrŸche durch Kreise.
Beispiel: 
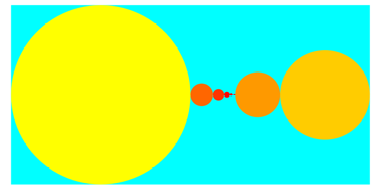
Dualbruch von 1/3 = 0. 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
Visualisierung:
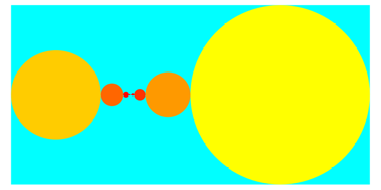
Exemplarisches Vorgehen:
Die erste
Nachkommastelle ist 0. Daher setzen wir den ersten Kreis mit dem Durchmesser 
ans obere Ende des Intervalls 
.
Die zweite
Nachkommastelle ist 1. Wir sehen den zweiten Kreis mit dem Durchmesser 
ans untere Ende des noch freien
Intervalls 
.
Die dritte
Nachkommastelle ist 0. Wir setzen den dritten Kreis mit dem Durchmesser 
ans obere Ende des noch freien Intervalls
.
Und so weiter und so
fort. Der Punkt 
ist immer im
Innern des noch freien Intervalls.
Wir haben von links und von rechts her eine Folge von immer kleiner werdenden Kreisen. Der Grenzpunkt ist bei einem Drittel.
2 Allgemein
Wir schreiben eine
reelle Zahl 
in der
Dualbruchdarstellung und beginnen die Visualisierung mit dem leeren Intervall 
.
Der n-te Kreis hat den Durchmesser 
. Wenn die n-te Nachkommastelle in der Dualbruchentwicklung 1
ist, setzen wir den n-ten Kreis
ans untere Ende des noch freien Intervalls, andernfalls ans obere Ende. Der
Punkt a ist immer im Innern der
auf dem Rand des noch freien Intervalls. Letzteres ist nur dann der Fall, wenn a eine abbrechende Dualbruchentwicklung hat.
Wir erhalten von links und von rechts her eine Folge von immer kleiner werdenden Kreisen. Der Grenzpunkt ist bei a.
3 Beispiele
3.1 Zehntel
In den folgenden
Beispielen ist 
.
0 = 0. 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.1 = 0. 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1
0.2 = 0. 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
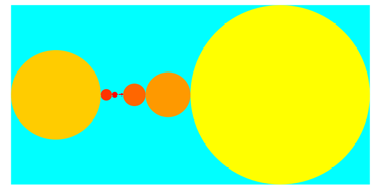
0.3 = 0. 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
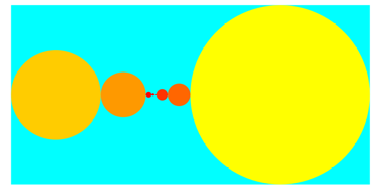
0.4 = 0. 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0
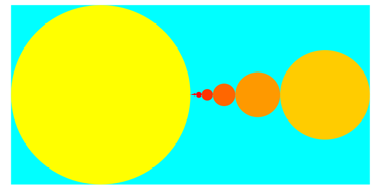
0.5 = 0. 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
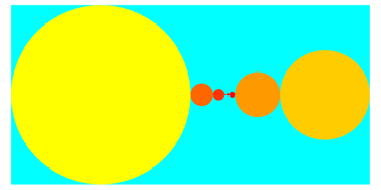
0.6 = 0. 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1
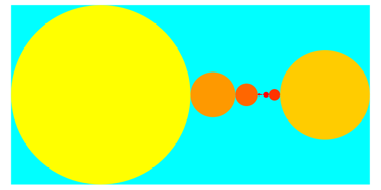
0.7 = 0. 1 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
0.8 = 0. 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
0.9 = 0. 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0
1 = 0. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3.2 StammbrŸche
Beispiele fŸr die
StammbrŸche 
.
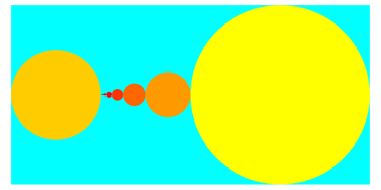
1/4 = 0. 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1/5 = 0. 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1/6 = 0. 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
1/7 = 0. 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0
1/8 = 0. 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3.3 Irrationale Zahlen
Bei irrationalen Zahlen ist die Dualbruchentwicklung aperiodisch.
FŸr 
erhalten wir:
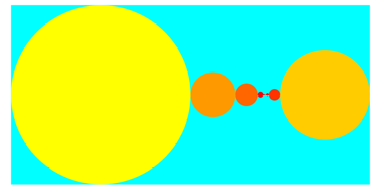
1/2*2^(1/2) = 0. 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 1 1 1 1
FŸr 
erhalten wir:
1/4*PI = 0. 1 1 0 0 1 0 0 1 0 0 0 0 1 1 1 1 1 1 0 1
Und schlie§lich noch
der Goldene Schnitt 
:
1/2*5^(1/2) - 1/2 = 0. 1 0 0 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 1 1