Hans Walser, [20190513]
DualitŠt
1 Worum geht es?
Gelenkmodell zur Illustration der DualitŠt bei regulŠren Netzen und sphŠrischen platonischen Figuren.
2 Grundprinzip
Wir arbeiten mit ăScherenŇ, also StŠben, welche in der Mitte gelenkig verbunden sind. An den Enden verbinden wir sie ebenfalls gelenkig mit weiteren Scheren.
3 Ebenes Beispiel: Dreiecke und Sechsecke
Die Abbildung 1 zeigt die Ausgangslange. Die Punkte sind Gelenke.

Abb. 1.1: Ausgangslage
Wir kšnnen nicht entscheiden, ob wir es mit Dreiecken oder Sechsecken zu tun haben.
Wenn wir jedoch die Gelenkpunkte auf den Kantenmitten der Sechsecke ins Innere der Sechsecke bewegen, werden Dreiecke optisch dominant (Abb. 1.2).

Abb. 1.2: Dreiecke
Die Abbildung 1.3 zeigt die Situation beim ă†berziehenŇ.
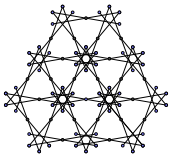
Abb. 1.3: †berzogene Dreiecke
Wenn wir umgekehrt, ausgehend von der Situation der Abbildung 1.1, die Gelenkpunkte auf den Kantenmitten der Dreiecke ins Innere der Dreiecke bewegen, werden Sechsecke optisch dominant (Abb. 1.4).
Diese Figur ist dual zur Figur der Abbildung 1.2 mit den Dreiecken.

Abb. 1.4: Sechsecke
Wir kšnnen auch hier źberziehen (Abb. 1.5).
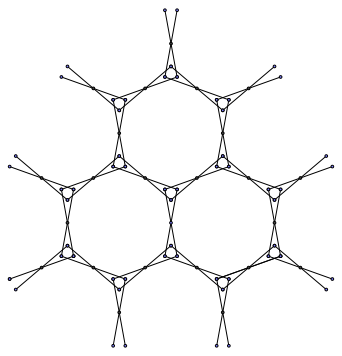
Abb. 1.5: †berzogene Sechsecke
Bei realen Modellen kšnnen die Gelenkpunkte nicht źber die Stangen gezogen werden. Ein †berziehen ist daher nicht mšglich.
4 SphŠrische Beispiele
Die Scheren sind aus MetallbŠndern gefertigt (Material aus der Verpackungsindustrie). Das Band ist ein halbes Inch breit (12.7mm). Der Lochabstand zwischen zwei Gelenken, also dem Mittelgelenk und einem Au§engelenk, betrŠgt drei Inch (76.2mm). Der Lochdurchmesser betrŠgt 3mm. Das Gelenk ist mit einer M3 Metallschraube und zwei gegeneinander fixierten Muttern realisiert. Die gesamte LŠnge eines Metallbandes betrŠgt 165.1 mm. Die MetallbŠnder werden etwas gekrźmmt.
4.1 Oktaeder und Hexaeder
Wir benštigen zwšlf Scheren, also 2 BŠnder, da Oktaeder und Hexaeder zwšlf Kanten haben.
Die Abbildung 2.1 zeigt die Ausgangslage. Es handelt sich um ein sphŠrisches Kuboktaeder, das aus acht gleichseiteigen sphŠrischen Dreiecken und sechs regelmŠ§igen sphŠrischen Vierecken besteht.

Abb. 2.1: Ausgangslage
Wenn wir nun die Gelenke auf den Kantenmitten der Vierecke ins Innere der Vierecke bewegen, ergibt sich ein sphŠrisches Oktaeder (Abb. 2.2).

Abb. 2.2: SphŠrisches Oktaeder
Wenn wir umgekehrt die Gelenkpunkte auf den Kantenmitten der Dreiecke ins innere der Dreiecke bewegen, ergibt sich ein sphŠrisches Hexaeder (Abb. 2.3)

Abb. 2.3: SphŠrisches Hexaeder
Oktaeder und Hexaeder sind zueinander dual.
Die TrŠgerkugeln der Abbildung 2.1 bis 2.3 haben verschiedene Durchmesser. Daher verŠndert sich auch die Krźmmung der MetallbŠnder. Diese mźssen daher etwas flexibel sein.
4.2 SphŠrisches Tetraeder
Das sphŠrische Tetraeder ist zu sich selbst dual.
Wir benštigen sechs Scheren, also zwšlf BŠnder, da das Tetraeder sechs Kanten hat.
Die Abbildung 3.1 zeigt die Ausgangslage. Diese Ausgangslage ist ein Oktaeder.

Abb. 3.1: Ausgangslage
Wir denken uns die acht Dreiecke des Oktaeders abwechslungsweise schwarz und wei§ gefŠrbt. Nun bewegen wir die Gelenke auf den Kantenmitten der schwarzen Dreiecke ins Innere der schwarzen Dreiecke. Die Abbildung 3.2 zeigt, wie das im Einzelnen aussieht.

Abb. 3.2: Zusammenschieben von drei Gelenken
So entsteht ein sphŠrisches Tetraeder (Abb. 3.3).

Abb. 3.3: SphŠrisches Tetraeder
Wenn wir analog mit den wei§en Dreiecken vorgehen, erhalten wir das duale Tetraeder.