Hans Walser, [20190425]

Dualsystem

1 Worum geht es?

Eine Visualisierung des Dualsystems.

2 Prinzip

Die Abbildung 1 zeigt das Prinzip. Jede der Figuren Tetraeder und Würfel kommt genau in der Hälfte der Felder vor.

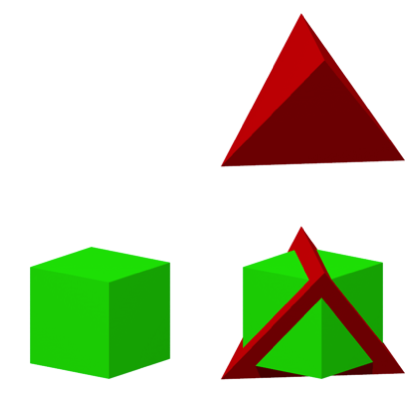
Abb. 1: Prinzip

3 Ausführliches Beispiel

Die Abbildung 2 zeigt ein ausführliches Beispiel. Jede der Figuren Tetraeder, Würfel, Oktaeder, Dodekaeder, Ikosaeder und Kugel kommt genau in der Hälfte der Felder vor.

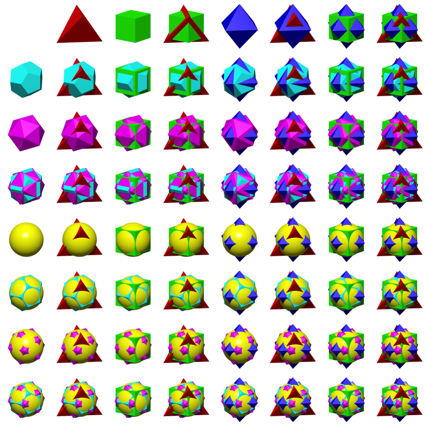
Abb. 2: Ausführliches Beispiel

In zwei Feldern, welche punktsymmetrisch zum Tabellenmittelpunkt liegen, kommen insgesamt alle sechs Körper je genau einmal vor.

4 Isometrische Axonometrie

Die Abbildung 3 zeigt dasselbe in isometrischer Axonometrie.

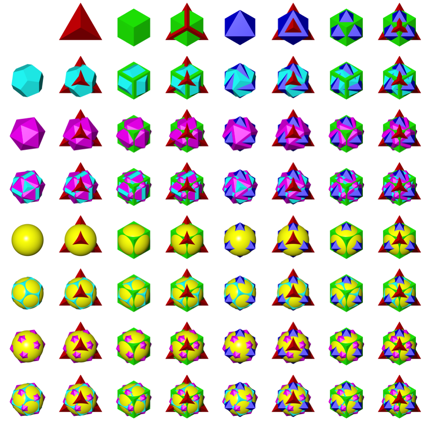
Abb. 3: Isometrische Axonometrie

5 Link zum Dualsystem

Wir ordnen jeder Teilfigur in der Abbildung 2 eine sechsstellige Dualzahl als Code zu. Die „Einer“ geben an, ob das Tetraeder vorkommt, die „Zweier“, ob der Würfel vorkommt, und so weiter. Reihenfolge von links nach rechts: Kugel, Ikosaeder, Dodekaeder, Oktaeder, Würfel, Tetraeder. Beispiel: in 100110 haben wir die Kugel, das Oktaeder und den Würfel, nicht aber das Ikosaeder, das Dodekaeder und den Tetraeder (die Teilfigur befindet sich in der fünften Zeile an siebenter Stelle).

Die Tabelle 1 entspricht der Abbildung 2.

000000	000001	000010	000011	000100	000101	000110	000111
001000	001001	001010	001011	001100	001101	001110	001111
010000	010001	010010	010011	010100	010101	010110	010111
011000	011001	011010	011011	011100	011101	011110	011111
100000	100001	100010	100011	100100	100101	100110	100111
101000	101001	101010	101011	101100	101101	101110	101111
110000	110001	110010	110011	110100	110101	110110	110111
111000	111001	111010	111011	111100	111101	111110	111111

Tab. 1: Duale Codierung

Zwei Codes, welche gegenüber der Tabellenmitte punktsymmetrisch liegen, unterscheiden sich in jeder Ziffer. Sie haben also die maximale Hamming-Distanz 6.

6 Kombinatorik

Den Tetraeder haben wir in jeder zweiten Spalte. Den Würfel in den Spalten 3 und 4 sowie 7 und 8. Das Oktaeder in der rechten Bildhälfte. Das Dodekaeder in jeder zweiten Zeile. Das Ikosaeder in den Zeilen 3 und 4 sowie 7 und 8. Die Kugel in der unteren Bildhälfte.

Die Anzahlen der in einem Feld erscheinenden Körper sind in der Tabelle 2 aufgelistet.

Die Tabelle ist symmetrisch. Die Einträge entsprechen den Quersummen der Einträge der Tabelle 1.

0	1	1	2	1	2	2	3
1	2	2	3	2	3	3	4
1	2	2	3	2	3	3	4
2	3	3	4	3	4	4	5
1	2	2	3	2	3	3	4
2	3	3	4	3	4	4	5
2	3	3	4	3	4	4	5
3	4	4	5	4	5	5	6

Tab. 2: Anzahlen der Körper in jedem Feld

Die Summe zweier Zahlen der Tabelle 2, welche zur Tabellenmitte punktsymmetrisch liegen, ist immer 6.

7 Geometrie

Die fünf platonischen Körper und die Kugel habe alle dieselbe Oberfläche. Das ist vom Autor so gewählt worden.

Weblinks

Hans Walser: Oberflächengleiche platonische Körper und Kugel

www.walser-h-m.ch/hans/Miniaturen/O/Oberflaechengleich/Oberflaechengleich.htm

Hans Walser: Oberflächengleiche platonische Körper und Kugel 2

www.walser-h-m.ch/hans/Miniaturen/O/Oberflaechengleich2/Oberflaechengleich2.htm