Hans Walser, [20190416], [20200115]
Dudeney
Idee: Patrik G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien
1 Worum geht es?
Studien und Daten zum ăHaberdasher ProblemŇ (Dudeney, 1903).
2 Zerlegungsgleichheit
Die Abbildung 1 zeigt eine gemeinsame Zerlegung eines gleichseitigen Dreiecks und eines flŠchengleichen Quadrates mit vier Teilen (nach Dudeney, 1903).
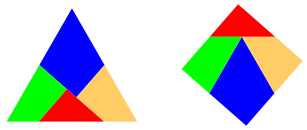
Abb. 1: Gemeinsame Zerlegung mit vier Teilen
3 Bezeichnungen und Daten
Wir setzen den gemeinsamen FlŠcheninhalt 1. Das Quadrat (Abb. 2) hat also die SeitenlŠnge 1.
Fźr die SeitenlŠnge s des gleichseitigen Dreieckes ergibt sich aus dem FlŠcheninhalt 1:
![]() (1)
(1)
Fźr die halbe SeitenlŠnge, die in der Abbildung 2 mehrfach erscheint, daher:
![]() (2)
(2)
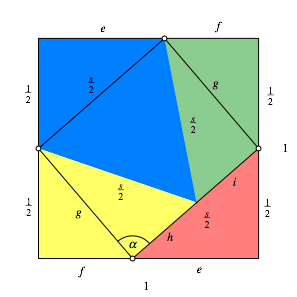
Abb. 2: Bezeichnungen
Weiter ist:
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Das schwarz eingezeichnete Viereck ist ein Parallelogramm. Sein spitzer Winkel ist:
![]() (6)
(6)
Das Parallelogramm ist also kein Rechteck.
Weiter ist:
![]() (7)
(7)
und
![]() (8)
(8)
Damit sind die vier Teile der Zerlegung konstruierbar.
4 Gelenkmodelle
4.1 Vier Gelenke
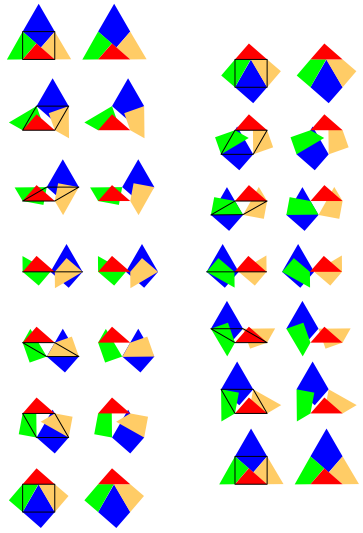
Abb. 4: Parallelogramm-Gelenkmodell
Wir denken uns in allen vier Ecken des Parallelogramms ein Gelenk. Die Abbildung 4 zeigt verschiedene Positionen des Parallelogramms.
Wir denken uns die Basis des Parallelogramms ortsfest. Dies ist auch die Basis des roten Dreieckes. Nun verdrehen wir eine anschlie§ende Seite des Parallelogramms. In der Abbildung 4 ist das eine Diagonale des grźnen Vierecks. Die zur festen Grundlinie des Parallelogramms parallele Seite ist eine Diagonale des blauen Viereckes. Die vierte Seite des Parallelogramms schlie§lich ist eine Diagonale des goldgelben Viereckes.
So kommen wir (linke Spalte der Abb. 4) vom gleichseitigen Dreieck zum Quadrat. Durch Weiterdrehen (rechte Spalte der Abb. 4) kommen wir schlie§lich wieder zum gleichseitigen Dreieck.
4.2 Anzahl der Ebenen
Wir sehen, dass sich die Puzzle-Teile źberlappen.
Fźr die linke Spalte der Abbildung 4 benštigen wir nur zwei Ebenen: eine vordere Ebene fźr rot-goldgelb und eine hintere Ebene fźr grźn-blau. Wenn wir also den Prozess der linken Spalte umkehren, kommen wir vom Quadrat zum gleichseitigen Dreieck zurźck. Somit kšnnen wir ein Modell Dreieck <–> Quadrat bauen, das mit zwei Ebenen und einer Richtungsumkehr arbeitet. Dies ist die Idee von Patrik G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien. Das Verfahren ist patentiert.
Die Animation 1 illustriert den Sachverhalt.

Animation 1
Bei der Modellierung beider Spalten der Abbildung 4 benštigen wir drei Ebnen: eine vorderste Ebene fźr rot, eine mittlere Ebene fźr grźn und goldgelb und eine hinterste Ebene fźr blau. Ein zyklisches Modell Dreieck –> Quadrat –> Dreieck benštigt also drei Ebenen. Die Animation 2 illustriert den Sachverhalt.

Animation
2
Weblinks
DITOH, Spezieller platonischer Kšrper
Animationen
http://www.walser-h-m.ch/hans/Miniaturen > Dudeney