Hans Walser, [20190527]
Dudeney
1 Worum geht es?
Ebenes Drehmodell zur Visualisierung der Zerlegung eines Quadrates in ein gleichseitiges Dreieck nach Dudeney. Kreisźberlagerungen
2 Die Zerlegung
Die Abbildung 1 zeigt die Zerlegung nach Dudeney.

Abb. 1: Zerlegung nach Dudeney
3 Gelenke
Es gibt verschiedene Gelenkmodelle, um den †bergang von Quadrat zum Dreieck zu zeigen. Alle mir bekannten Gelenkmodelle arbeiten mit den in der Abbildung 2 eingezeichneten Gelenkpunkten.
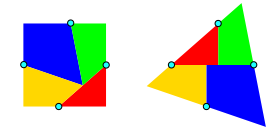
Abb. 2: Gelenkpunkte
Die vier Gelenkpunkte bilden ein Parallelogramm. Dieses ist aber kein Rechteck. Die Abweichung vom rechten Winkel betrŠgt allerdings nur etwa 0.5964ˇ und kann daher von blo§em Auge zunŠchst nicht wahrgenommen werden.
4 Drehpunkte
Beim Quadrat legen wir in der Mitte zwischen je zwei Gelenkpunkten einen Drehpunkt fest. Vier dieser Drehpunkte sind also die Kantenmitten des Parallelogramms, der fźnfte sein Mittelpunkt (Abb. 3). Man beachte, dass der Mittelpunkt der Hypotenuse des roten Dreiecks sich nicht in der gemeinsamen Ecke des grźnen, blauen und goldenen Teils befindet. Dies ist eine Folge der Abweichung des Parallelogramms vom Rechteck.
Nun drehen wir jedes Puzzleteil um eine der Kantenmitten um 180ˇ.
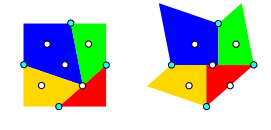
Abb. 3: Drehungen
Die entstehende Figur ist noch nicht das gleichseitige Dreieck. Wenn wir aber das rote und das blaue Teil noch zusŠtzlich um den Mittelpunkt des Parallelogramms um 180ˇ drehen, kommen wir hin (Abb. 4).
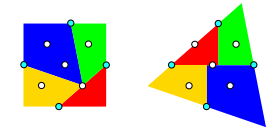
Abb. 4: Drehung um Mittelpunkt

Die Animation1 beschreibt den Vorgang.
5 Analyse der Drehungen. Bahnkurven
Das grźne und das goldene Teil werden einfach gedreht. Die Bahnkurven sind Kreise.
Beim roten und beim blauen Teil haben wir eine †berlagerung von zwei Drehungen. Das erleben wir etwa, wenn auf einem drehenden Karussell sich ein zusŠtzlich drehendes Binnenkarussell befindet. Das rote und das blaue Teil beschreiben eine Art Salto.
Jedes Teil hat eine Ecke mit einem rechten Winkel, die Ecken des Quadrates. Die Abbildung 5 gibt die Bahnkurven dieser Eckpunkte. Wir sehen, dass beim grźnen und beim goldenen Teil noch je zwei weitere Eckpunkte auf der zugehšrigen Bahnkurve liegen. Diese Bahnkurven sind Kreise. Die Bahnkurven des roten und des blauen Teils haben einen doppelten Umlauf und einen Doppelpunkt. Es handelt sich hier um (verallgemeinerte) Strophoiden.
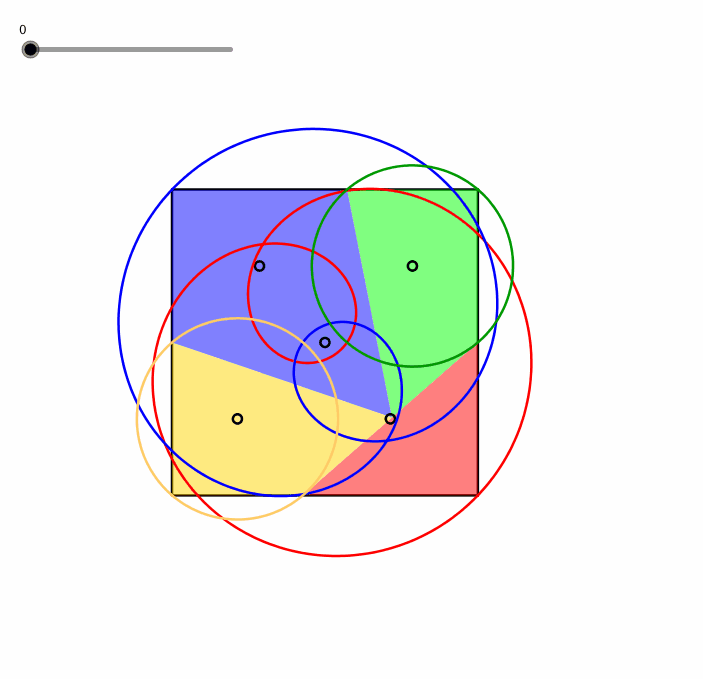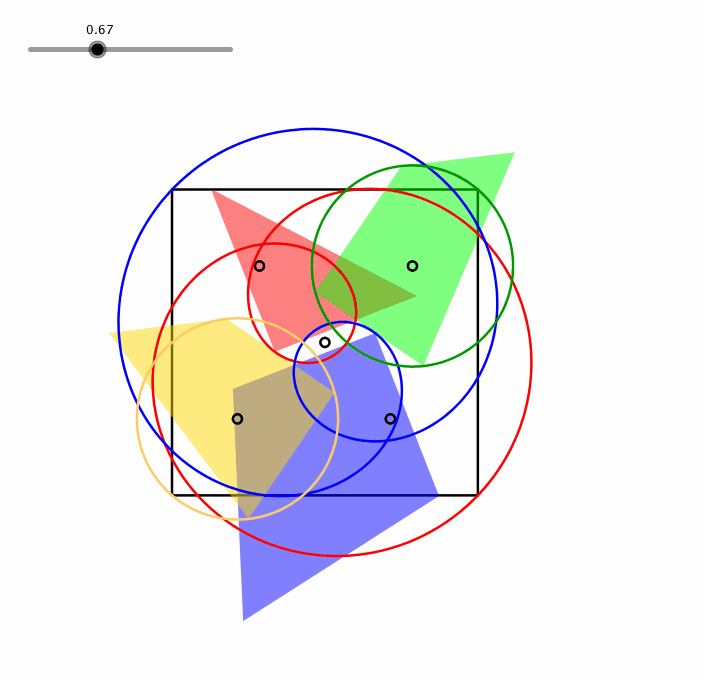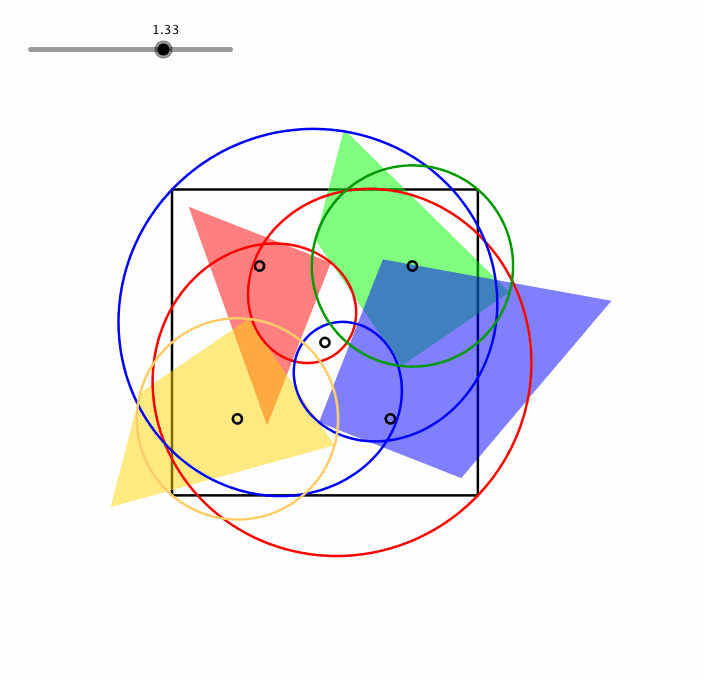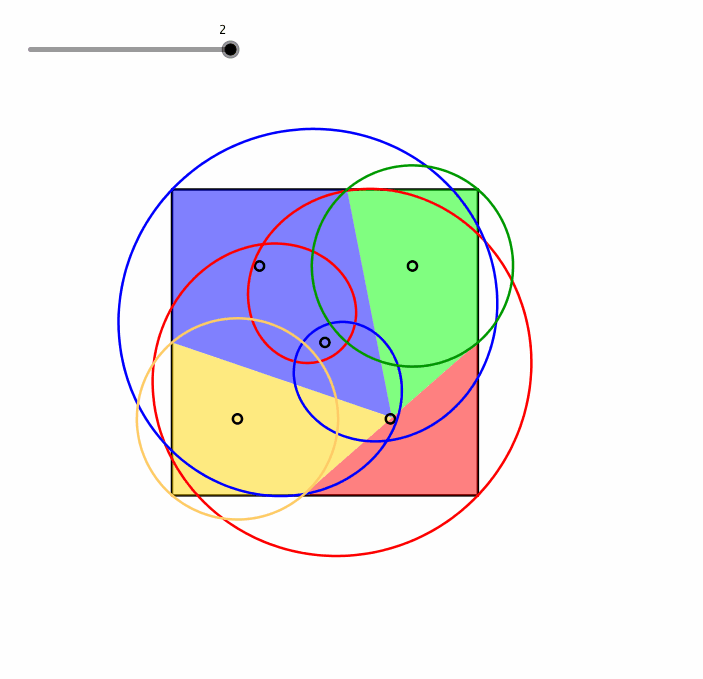
In der Animation2 sehen wir das Gleiten der Eckpunkte auf diesen Bahnkurven.
Abb. 5: Bahnkurven der Ecken mit rechten Winkeln
Das grźne, blaue und goldene Teil haben auch je eine Ecke mit einem 60ˇ-Winkel, die Ecken des gleichseitigen Dreiecks. Die Abbildung 6 zeigt die Bahnkurven dieser drei Punkte.

In der Animation3 sehen wir das Gleiten der Eckpunkte auf diesen Bahnkurven.

Abb. 6: Bahnkurven der Ecken mit 60ˇ-Winkeln
Weblinks
DITOH, Spezieller platonischer Kšrper
Hans Walser: Sechseckpuzzle
http://www.walser-h-m.ch/hans/Miniaturen/S/Sechseckpuzzle/index.html
Hans Walser: Kreuzpuzzle
http://www.walser-h-m.ch/hans/Miniaturen/K/Kreuzpuzzle2/index.html
Hans Walser: Frederickson
http://www.walser-h-m.ch/hans/Miniaturen/F/Frederickson/index.html
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney2/Dudeney2.htm
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney3/index.html