Hans Walser, [20200912]
Durcevic
Ausarbeitung einer Idee von Zvonimir Durcevic, Wien
1 Ellipse mit Leitkreis
Auf einem Kreis mit Mittelpunkt F1 wŠhlen wir einen Punkt P (Abb. 1.1a). Diese beiden Punkte verbinden wir. Und wir wŠhlen einen zusŠtzlichen Punkt F2 (Abb. 1.1b).

Abb. 1.1: Konstruktionsbeginn
Nun schneiden wir die Strecke F1P mit der Mittelsenkrechten der Strecke F2P. Den Schnittpunkt bezeichnen wir mit E (Abb. 1.2a).

Abb. 1.2: Konstruktion der Ellipse
Wenn nun der Punkt P auf dem Kreis variiert, beschreibt der Punkt E seinerseits eine Ellipse (Abb. 1.2b). Die Mittelsenkrechte ist jeweils die Ellipsentangente in E.
Die Stimmigkeit der Konstruktion ergibt sich daraus, dass die Strecken EP und EF2 gleich lang sind. Daher ist die Summe der StreckenlŠngen F1P und F2P gleich dem Kreisradius und daher konstant.
2 Die Eikurve
Nun sei Z der Mittelpunkt der Strecke EP (Abb. 2a). Bei Variation von P auf dem Kreis beschreibt Z eine eifšrmige Kurve (Abb. 2b).
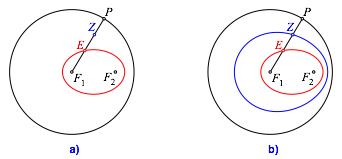
Abb. 2: Eikurve
Die Animation 1 illustriert das Verhalten der Kurve bei Variation von F2. Wir haben nicht immer eine eifšrmige Kurve.
Wenn F2 au§erhalb des Kreises liegt, ergibt sich statt der Ellipse eine Hyperbel. Und die blaue Kurve ist nicht mehr geschlossen.
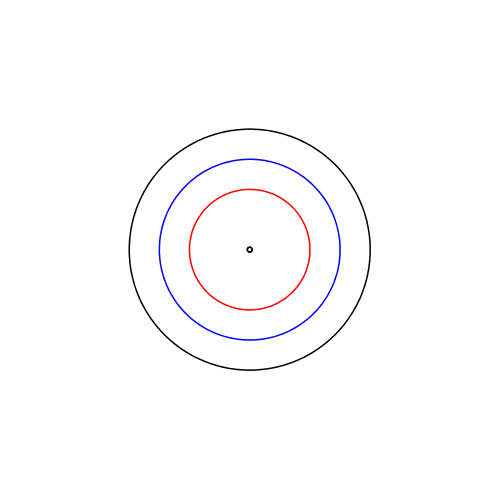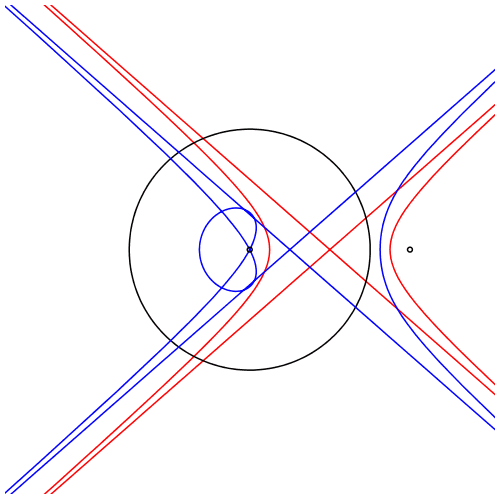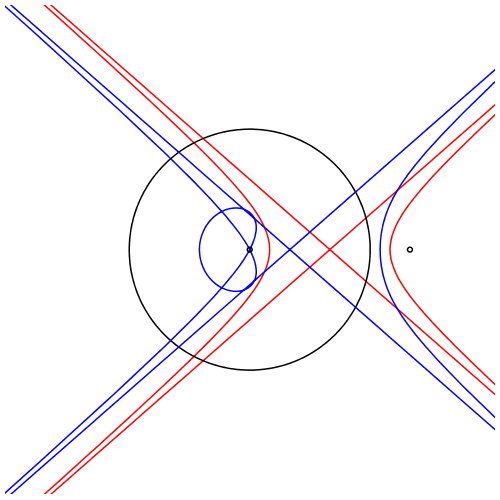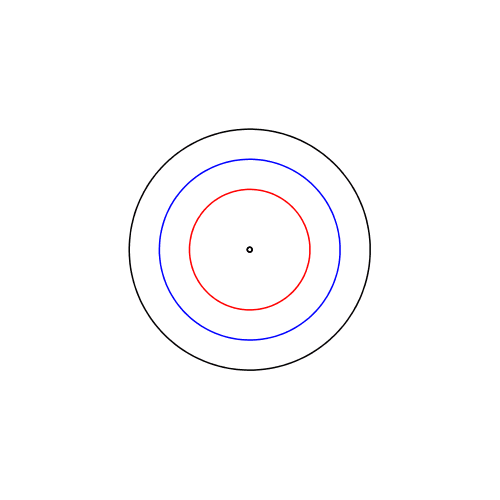
Animation 1: Variation des zweiten Brennpunktes
3 Variation des Teilpunktes
In der Animation 2 ist der Punkt Z nicht mehr Mittelpunkt, sondern erster Drittelpunkt der Strecke EP.
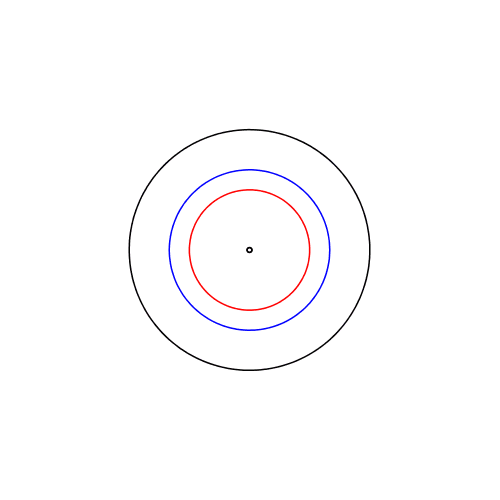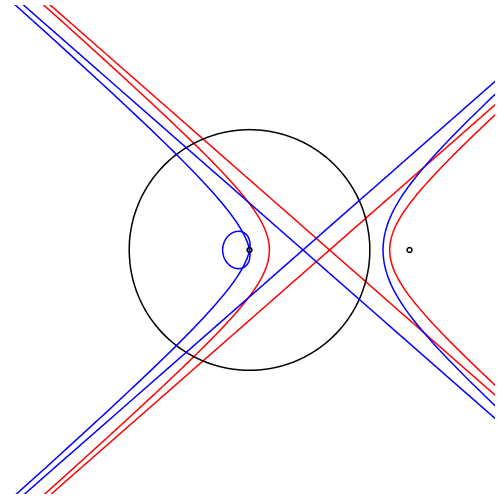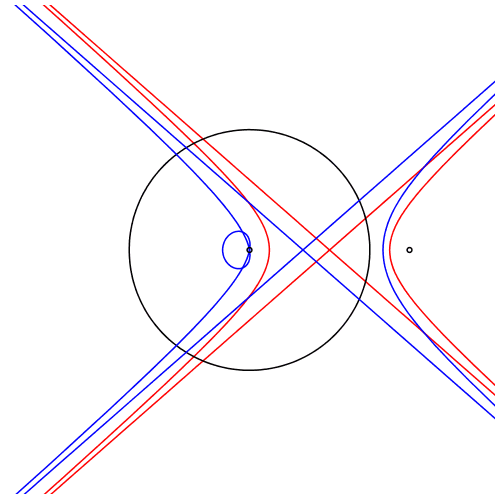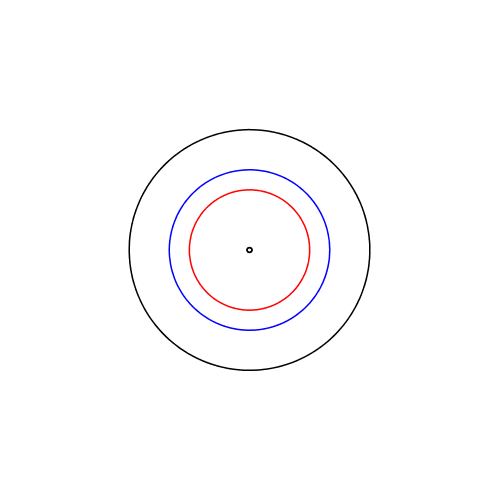
Animation 2: Drittelpunkt
Websites
Zvonimir Durcevic
http://www.zvone.com/math/conic-sections/fixed_circle.html