Hans Walser, [20141211]
Eckige Spirale
1 Rekursive Definition mit Crossprodukt
Wir definieren eine Vektorfolge rekursiv wie folgt:
Startvektoren:
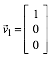 ,
, 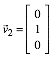
Rekursion (Erinnerung an die Fibonacci-Rekursion):
![]()
Wir erhalten der Reihe nach:
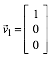 ,
, 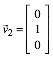 ,
, 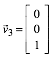 ,
, 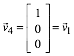 ,
, 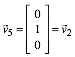
Wir erhalten eine periodische Folge mit der PeriodenlŠnge 3:
![]()
Die Abbildung 1 zeigt die ersten neun Vektoren der Folge als Vektorzug. Der schwarze Einheitswźrfel ist zur rŠumlichen Orientierung eingezeichnet.
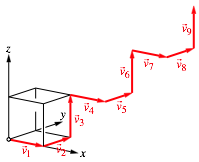
Abb. 1: Vektorzug
Die Vektoren bilden eine eckige Spirale mit Rechtsgewinde.
Die Spirale lŠuft auf einem Dreikant mit einem gleichseitigen Dreieck als Querschnitt (Abb. 2).
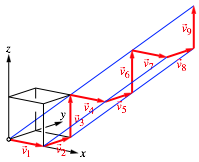
Abb. 2: Dreikant
2 Modellierung mit Wźrfeln
2.1 KantenlŠnge zwei
Die Abbildung 3 zeigt eine Modellierung mit Wźrfeln. Dabei sind in jeder Richtung jeweils zwei Wźrfel verwendet worden. Die Vektoren der Abbildung 2 verlaufen jeweils von Wźrfelmitte zu Wźrfelmitte. Sie sind also gleich lang wie die Wźrfelkante.
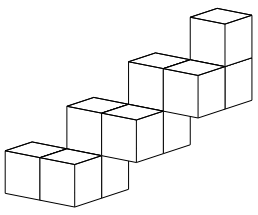
Abb. 3: Modellierung mit Wźrfeln
Die Abbildung 4 zeigt das Foto eines entsprechenden Papiermodells (Flechtmodell).

Abb. 4: Papiermodell
Die Spiralachse verlŠuft durch die Wźrfel hindurch.
2.2 KantenlŠnge vier
2.2.1 Eine Spirale
Damit die Spiralachse nicht durch die Wźrfel verlŠuft, muss mit KantenlŠnge vier gearbeitet werden (Abb. 5). Die Vektoren sind gleich lang wie die dreifache Wźrfelkante.
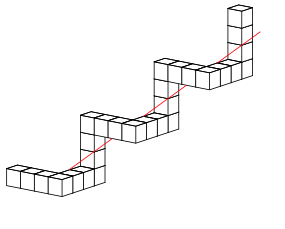
Abb. 5: Spiralachse
Die Spiralachse (rot in Abbildung 5) geht haarscharf an den Wźrfeln vorbei.
2.2.2 Zwei Spiralen
Nun kann auch noch eine zweite kongruente Spirale eingefźgt werden (Abb. 6). Sie ist gegenźber der ersten Spirale um 120ˇ verdreht.
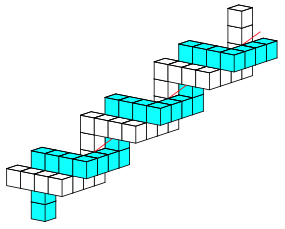
Abb. 6: Zwei Spiralen
2.2.3 Drei Spiralen
Schlie§lich kann auch eine dritte Spirale eingebaut werden (Abb. 7). Im Innern der Figur hat es wźrfelfšrmige HohlrŠume, in denen die Spiralachse durchgeht. Solche HohlrŠume sind in der Abbildung 6 erkennbar.
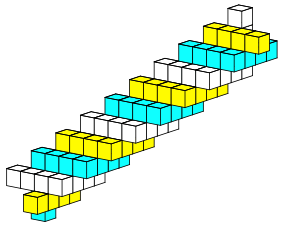
Abb. 7: Drei Spiralen
Die drei Spiralen sitzen fest ineinander.
Die Abbildung 8 zeigt ein Papiermodell.

Abb. 8: Papiermodell
Da die drei Spiralen fest ineinander sitzen, mussten sie vor Ort gleichzeitig aufgebaut werden.
3 DNA
Die Abbildung 6 mit den zwei um 120ˇ verdrehten Spiralen erinnert an die DNA-Spirale (Abb. 9).

Abb. 9: DANN
Auch hier kšnnte rein geometrisch eine dritte Spirale eingefźgt werden (Abb. 10).
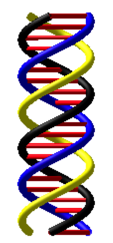
Abb. 10: Dritte Spirale