Hans Walser, [20161022]
Eckige Spiralen
1 Worum geht es?
Es werden Spiralen vorgestellt, die aus rechtwinkligen Dreiecken aufgebaut sind.
2 Rekursion
Die Dreiecke werden rekursiv definiert. Bezeichnungen gemŠ§ Abbildung 0.
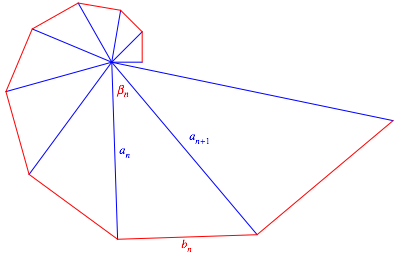
Abb. 0: Bezeichnungen
Auf jeden Fall soll fźr an die Rekursion
(1)
mit dem Startwert a0 = 1 gelten.
Fźr bn kšnnen wir irgend eine Bedingung wŠhlen. Entsprechend Šndert das Aussehen der Spirale.
3 Beispiele
3.1 Der Klassiker
Fźr bn = an ergibt sich die klassische Spirale der Abbildung 2.
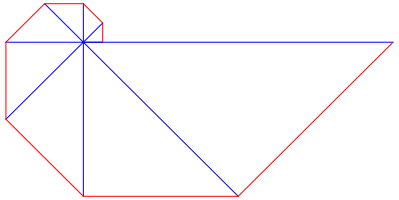
Abb. 1: Klassiker
Es ist
durchgehend 
. Weiter ist daher 
. Wir haben ein exponentielles Wachstum. Die Spirale
ist eine logarithmische Spirale mit folgender Drehstrecksymmetrie: Drehung um
45ˇ mit gleichzeitiger Streckung mit 
ist eine
Deckabbildung der Spirale.
3.2 Die Wurzelspirale
Fźr bn = 1 erhalten wir die ăWurzelspiraleŇ (Abb. 2.1).
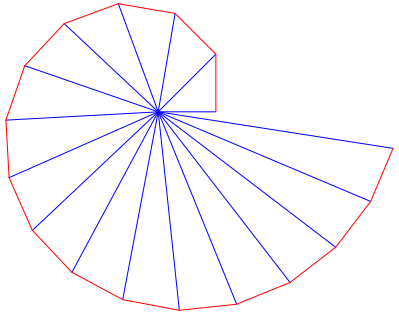
Abb. 2.1: Wurzelspirale
Es ist 
.
Die Wurzelspirale approximiert eine archimedische Spirale (Abb. 2.2):
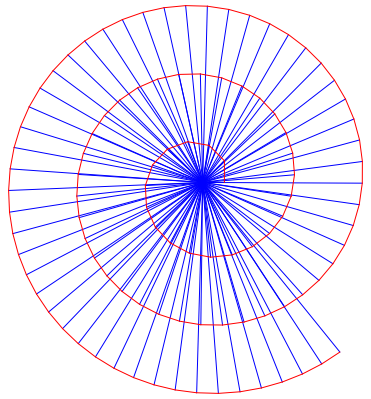
Abb. 2.2: Archimedische Spirale
3.3 Fibonacci-Spirale
Mit
(2)
erhalten wir die Spirale der Abbildung 3.
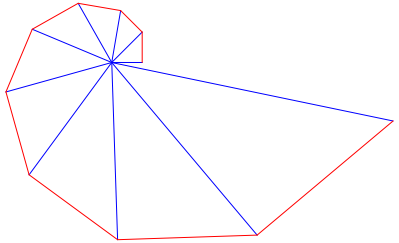
Abb. 3: Fibonacci-Spirale
Die Tabelle 1 gibt die Werte fźr an und bn.
|
n |
an |
an2 |
bn |
bn2 |
|
|
1 |
1.00000 |
1 |
1.00000 |
1 |
45.00000 |
|
2 |
1.41421 |
2 |
1.00000 |
1 |
35.26439 |
|
3 |
1.73205 |
3 |
1.41421 |
2 |
39.23152 |
|
4 |
2.23607 |
5 |
1.73205 |
3 |
37.76124 |
|
5 |
2.82843 |
8 |
2.23607 |
5 |
38.32882 |
|
6 |
3.60555 |
13 |
2.82843 |
8 |
38.11293 |
|
7 |
4.58258 |
21 |
3.60555 |
13 |
38.19552 |
|
8 |
5.83095 |
34 |
4.58258 |
21 |
38.16399 |
|
9 |
7.41620 |
55 |
5.83095 |
34 |
38.17604 |
|
10 |
9.43398 |
89 |
7.41620 |
55 |
38.17144 |
|
11 |
12.00000 |
144 |
9.43398 |
89 |
38.17319 |
|
12 |
15.26434 |
233 |
12.00000 |
144 |
38.17252 |
|
13 |
19.41649 |
377 |
15.26434 |
233 |
38.17278 |
|
14 |
24.69818 |
610 |
19.41649 |
377 |
38.17268 |
|
15 |
31.41656 |
987 |
24.69818 |
610 |
38.17272 |
Tab. 1: Daten der Fibonacci-Spirale
Offenbar ist mit der Schreibweise Fn fźr die Fibonacci-Zahlen:
(3)
Daher der Name Fibonacci-Spirale.
Die
Winkel 
haben
einen Limes:
(4)
Hier erscheint der Goldene Schnitt. Die rechtwinkligen Dreiecke werden sich also fźr wachsendes n immer Šhnlicher. Wir approximieren eine logarithmische Spirale.
3.4 Fibofibonacci-Spirale
Mit
(5)
erhalten wir die Spirale der Abbildung 4.
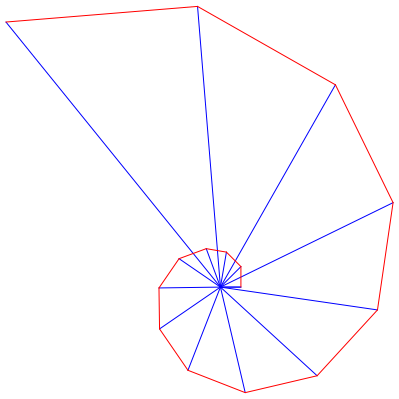
Abb. 4: Fibofibonacci-Spirale
Die Tabelle 2 gibt die relevanten Daten.
|
n |
an |
an2 |
bn |
bn2 |
|
|
0 |
1.00000 |
1 |
0.00000 |
0 |
0.00000 |
|
1 |
1.00000 |
1 |
0.00000 |
0 |
0.00000 |
|
2 |
1.00000 |
1 |
1.00000 |
1 |
45.00000 |
|
3 |
1.41421 |
2 |
1.00000 |
1 |
35.26439 |
|
4 |
1.73205 |
3 |
1.00000 |
1 |
30.00000 |
|
5 |
2.00000 |
4 |
1.41421 |
2 |
35.26439 |
|
6 |
2.44949 |
6 |
1.73205 |
3 |
35.26439 |
|
7 |
3.00000 |
9 |
2.00000 |
4 |
33.69007 |
|
8 |
3.60555 |
13 |
2.44949 |
6 |
34.19086 |
|
9 |
4.35890 |
19 |
3.00000 |
9 |
34.53758 |
|
10 |
5.29150 |
28 |
3.60555 |
13 |
34.26994 |
|
11 |
6.40312 |
41 |
4.35890 |
19 |
34.24491 |
|
12 |
7.74597 |
60 |
5.29150 |
28 |
34.33816 |
|
13 |
9.38083 |
88 |
6.40312 |
41 |
34.31648 |
|
14 |
11.35782 |
129 |
7.74597 |
60 |
34.29377 |
Tab. 2: Fibofibonacci-Zahlen
Eine Schlźsselrolle spielt die Zahl:
(6)
Dies ist die reelle Lšsung der kubischen Gleichung:
(7)
Die
Winkel 
haben den
Limes:
(8)