Hans Walser, [20210312]
Eckige archimedische Spirale
Bearbeitung und Adaptation der Aufgabe 56-667 von Thomas Jahre
1 Worum geht es?
Beispiel einer einfachen eckigen archimedischen Spirale.
2 Konstruktion der Spirale
Die eckige Spirale (Abb. 1) wird definiert durch die Punkte:
![]() (1)
(1)
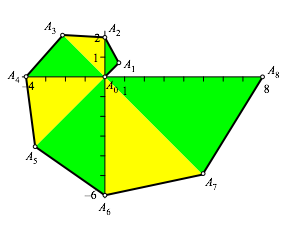
Abb. 1: Die eckige Spirale
3 Zugehšrige archimedische Spirale
Die Eckpunkte liegen auf der archimedischen Spirale (Abb. 2):
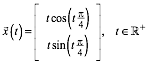 (2)
(2)
Abb. 2: Archimedische Spirale
4 LŠngenberechnung
Fźr die LŠnge sn der Strecke von An-1 nach An erhalten wir mit dem Kosinussatz:
![]() (3)
(3)
Fźr die GesamtlŠnge gn von A0 bis An entsprechend:
![]() (4)
(4)
Ich habe keine geschlossene Formel dafźr gefunden.
Die Tabelle 1 gibt die ersten numerischen Werte.
|
n |
GesamtlŠnge |
|
1 |
1 |
|
2 |
2.473625758 |
|
3 |
4.598412482 |
|
4 |
7.432038649 |
|
5 |
10.99795070 |
|
6 |
15.30765987 |
|
7 |
20.36760358 |
|
8 |
26.18172780 |
Tab.1 : GesamtlŠngen
5 FlŠchenberechnung
Fźr den FlŠcheninhalt Fn des Dreiecks A0An-1An berechnen wir:
![]() (5)
(5)
Daraus ergibt sich fźr die GesamtflŠche Gn:
![]() (6)
(6)
Die Tabelle 2 gibt die ersten numerischen Werte.
|
n |
GesamtflŠche |
|
2 |
.7071067810 |
|
3 |
2.828427124 |
|
4 |
7.071067810 |
|
5 |
14.14213562 |
|
6 |
24.74873734 |
|
7 |
39.59797974 |
|
8 |
59.39696960 |
Tab. 2: GesamtflŠchen
6 Bildergalerie
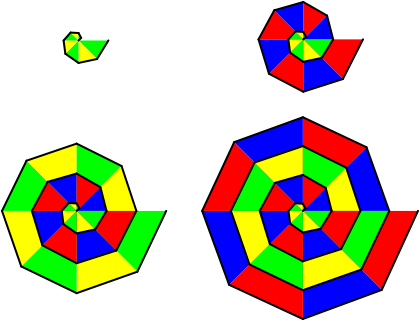
Abb. 3: Bildergalerie
Website
Thomas Jahre
https://www.schulmodell.eu/images/stories/mathe/wochenaufgabe/667.jpg