Hans Walser, [20080214b]
Ecktransversalen im Dreieck
1 Eingangsbeispiel
In einem Dreieck werden alle drei Seiten gedrittelt und dann die Ecktransversalen gemŠ§ Figur eingezeichnet.
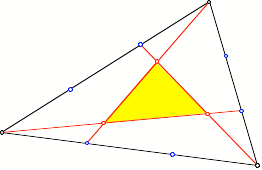
Ecktransversalen
Dann entsteht in der
Mitte ein Dreieck, dessen FlŠche 
der gro§en
DreiecksflŠche ist.
Das Problem soll zum ersten Mal 1912 in St. Petersburg in einer PrŸfung gestellt worden sein (vgl. [Alexanderson/Ross 2007], S. 279).
2 Lšsung im Dreiecksraster
Wir betten das kleine
Dreieck in einen Dreiecksraster ein.
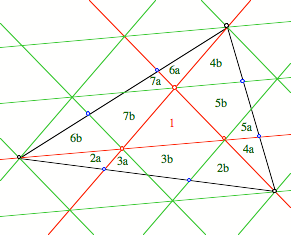
Dreiecksraster
Dann sehen wir, dass
das gro§e Dreieck genau 7 kleine Dreiecke enthŠlt. Aus SymmetriegrŸnden kšnnen
wir nŠmlich die Teile na und nb, 
, jeweils zu einem kleinen Dreieck zusammenfŸgen.
3
Rechnerische Lšsung und Verallgemeinerung
Das Problem ist affin
invariant, wir kšnnen uns also auf ein regulŠres Dreieck in der angegebenen
Disposition beschrŠnken.
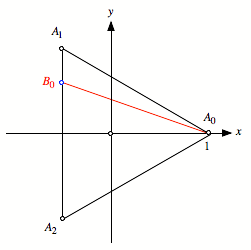
Standardisierte Version
Das Dreieck hat die
Eckpunktskoordinaten 
. Wir fŸhren nun ein allgemeines TeilverhŠltnis 
ein. Im Eingangsbeispiel
war 
.
Die Idee ist nun
folgende: Das kleine Dreieck ist wiederum ein regulŠres, der Abstand der
Transversale 
ist der
Inkreisradius dieses Dreiecks. Damit sind die FlŠchenverhŠltnisse berechenbar.
Die Transversale 
hat die
Gleichung:
und damit die Hessesche
Normalform:
FŸr den Abstand vom
Ursprung und damit fŸr den Inkreisradius 
des kleinen Dreieckes
erhalten wir daraus:
Das gro§e
Ausgangsdreieck hat den Inkreisradius 
; das RadienverhŠltnis ist also:
und das
FlŠchenverhŠltnis 
das Quadrat
davon:
Beispiele:
Weiter ist:
Dies ist auch
geometrisch klar.
Funktionsgraf:
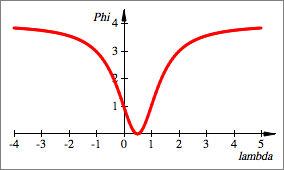
Literatur:
[Alexanderson/Ross
2007] Alexanderson,
Gerald L. and Peter Ross: The Harmony of the World. 75 Years of Mathematics Magazine. The Mathematical Association of
America. 2007. ISBN 978-0-88385-560-7