Hans Walser, [20190602]

Eddy

1 Worum geht es?

Ein Satz von Eddy gibt Anlass zu einer Invarianz von Flächenquadratsummen. Formal ist es eine Analogie zum Satz von Pythagoras, spielt aber im vierdimensionalen Raum.

2 Der Satz von Eddy

Die Halbierende des rechten Winkels im rechtwinkligen Dreieck zerlegt das Hypotenusenquadrat in zwei kongruente Teile (Abb. 1).

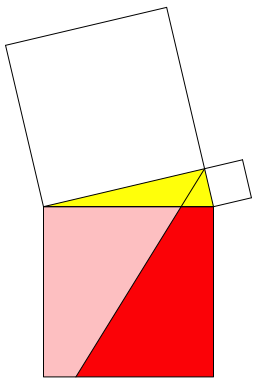
Abb. 1: Der Satz von Eddy

3 Der elegante Beweis

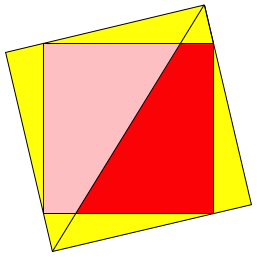
Abb. 2: Beweis ohne Worte

4 Der weniger elegante Beweis

Zunächst erinnern wir uns an folgenden Sachverhalt. In einem (beliebigen) Dreieck halbieren die Winkelhalbierenden je den Umkreisbogen über der Gegenseite (Abb. 3). Zu halben Winkel gehören halbe Peripheriebögen.

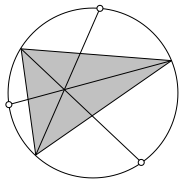
Abb. 3: Winkelhalbierende halbieren die Umkreisbögen

In unserem Sonderfall des rechtwinkligen Dreiecks ist der Umkreis der Thaleskreis. Der Mittelpunkt des Bogens über (anschaulich: „unter“) der Hypotenuse ist auch der Mittelpunkt des Hypotenusenquadrates (Abb. 4). Eine Gerade durch den Quadratmittelpunkt zerlegt das Quadrat in zwei kongruente Teile.

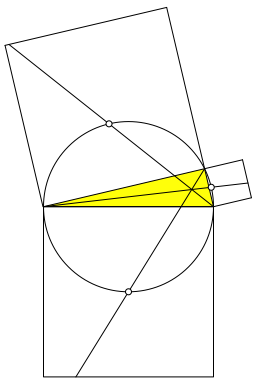
Abb. 4: Mittelpunkt des Hypotenusenquadrates

Damit ist der Satz von Eddy bewiesen.

Man beachte, dass die Bogenmitten über den Katheten nicht die Mittelpunkte der Kathetenquadrate sind.

5 Die äußere Winkelhalbierende

Die äußere Winkelhalbierende des rechten Winkels halbiert die beiden Kathetenquadrate. Damit ergibt sich eine lustige Version des Satzes von Pythagoras (Abb. 5).

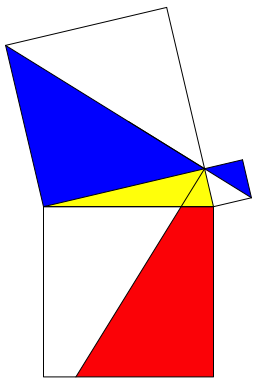
Abb. 5: Blau = rot

6 Schnitt mit dem Thaleskreis

Die äußere Winkelhalbierende des rechten Winkels schneidet den Thaleskreis in einem Punkt im inneren des größeren Kathetenquadrates (Abb. 6).

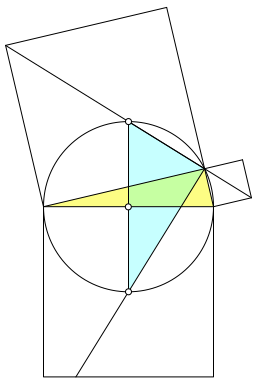
Abb. 6: Schnitt mit Thaleskreis

Dieser Punkt liegt auf der Mittelsenkrechten der Hypotenuse und gibt Anlass zu einem zweiten rechtwinkligen Dreieck (hellblau in Abb. 6).

7 Der Flächensatz

Wir bezeichnen mit r den Radius des Thaleskreises. und seien die Flächeninhalte der beiden rechtwinkligen Dreiecke.

Es gilt:

(1)

Die Formel (1) erinnert an den Satz von Pythagoras, spielt aber in der Dimension vier. Daher kann die Situation nicht zweidimensional illustriert werden. Es gibt daher auch keinen Zerlegungsbeweis.

8 Beweis des Flächensatzes

Wir arbeiten mit dem in der Abbildung 7 eigezeichneten Winkel t.

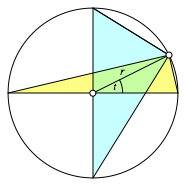
Abb. 7: Beweisfigur

Das gelbe Dreieck hat die Hypotenusenlänge 2r und die dazu senkrechte Höhe . Daher ist:

(2)

Analog:

(3)

Durch Quadrieren und Addieren von (2) und (3) ergibt sich (1).

Literatur

Zeuge, Wolfgang (2018): Nützliche und schöne Geometrie. Eine etwas andere Einführung in die Euklidische Geometrie. Springer Spektrum. ISBN 978-3-658-22832-3