1 Was sind Einrad-Wege?

Einrad-Wege können von einem Fahrrad mit zwei Rädern so abgefahren werden, dass die Spur des hinteren Rades die Spur des vorderen Rades deckt. Das sieht dann so aus, wie wenn wir die Spur eines Einrades hätten.

Die Schleppkurve ist also kongruent zur Zugkurve.

Für die umgekehrte Bewegungsrichtung gilt das Schubkarren-Modell: Auf einem Einrad-Weg kann der Schubkarrenpilot immer in der Spur des Schubkarrenrades gehen.

Das ist auch die Situation des Rückwärts-Einparkens.

Der einfachste Einrad-Weg ist die Gerade.

Es werden weitere Beispiele von Einrad-Wegen gezeigt.

2 Beispiele

2.1 Gestauchte Gaußsche Glockenkurve

Wir starten mit der Kurve:

(1)

Der Tangens dient dazu, die reellen Zahlen ins Intervall [0, 1] zu bringen. Die Abbildung 1 zeigt die Startkurve.

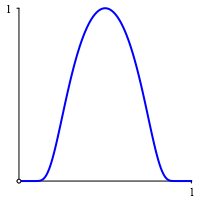
Abb. 1: Startkurve

Die Startposition des Fahrrades sei so, dass sich das Vorderrad in (1, 0) und das Hinterrad in (0, 0) befindet.

Nun setzen wir in jedem Kurvenpunkt eine Tangente an und tragen in Laufrichtung den Abstand 1 ab. Die Endpunkte der Tangentenabschnitte bilden die erste Iteration der Startkurve (rot in Abb. 2).

Abb. 2: Tangenten und erste Iteration

Wenn sich nun das Vorderrad auf der roten Kurve bewegt, fährt das Hinterrad auf der blauen Startkurve.

Die Abbildung 3 zeigt die Situation ohne die Tangenten.

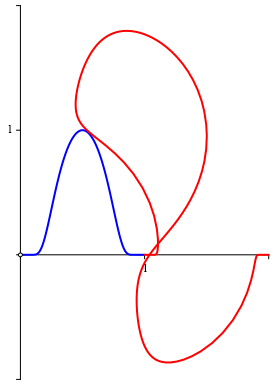
Abb. 3: Startkurve und erste Iteration

Wir können nun entsprechend weitere Iterationen anfügen. Die Abbildung 4 zeigt alternierend in blau und rot die Startkurve und die ersten drei Iterationen. Eine recht „wilde“ Sache.

Abb. 4: Startkurve und die ersten drei Iterationen

Wir modifizieren die Startkurve, indem wir die Amplitude auf 1% reduzieren:

(2)

Die Abbildung 5 zeigt die Startkurve, eine ganz sanfte Bodenwelle.

Abb. 5: Modifizierte Startkurve

Trotzdem werden die Iterationen „wild“ (Abb. 6).

Abb. 6: Startkurve und Iterationen

2.2 Zweites Beispiel

Wir arbeiten mit der Startkurve (Abb. 7):

(3)

Abb. 7: Zweites Beispiel, Startkurve

Die Abbildung 8 zeigt die erste und die zweite Iteration. Die dritte Iteration hat mein Computer nicht mehr geschafft.

Abb. 8: Startkurve, erste und zweite Iteration

Literatur

Nesky, Amy and Redwood, Clara (2016): Discrete and Smooth Bicycle „Unicycle“ Paths. The College Mathematics Journal, Vol. 47, No. 3, May 2016. 180-189.