Hans Walser, [20240606]

Ellipse

Anregung: Peter Gallin, Zürich

1 Worum es geht

Eine Konstruktion auf der Basis eines beliebigen Dreiecks führt zu sechs auf einer Ellipse liegenden Punkten. Dabei spielen gleichseitige Dreiecke eine zentrale Rolle.

Mit DGS verifiziert, und einen formalen Beweis bin ich dankbar.

2 Konstruktion

Den Seiten eines beliebigen Dreiecks setzen wir je zwei x-förmig angeordnete gleichseitige Dreiecke an (Abb. 1). Die Außenecken der gleichseitigen Dreiecke markieren wir im Wechsel blau und rot.

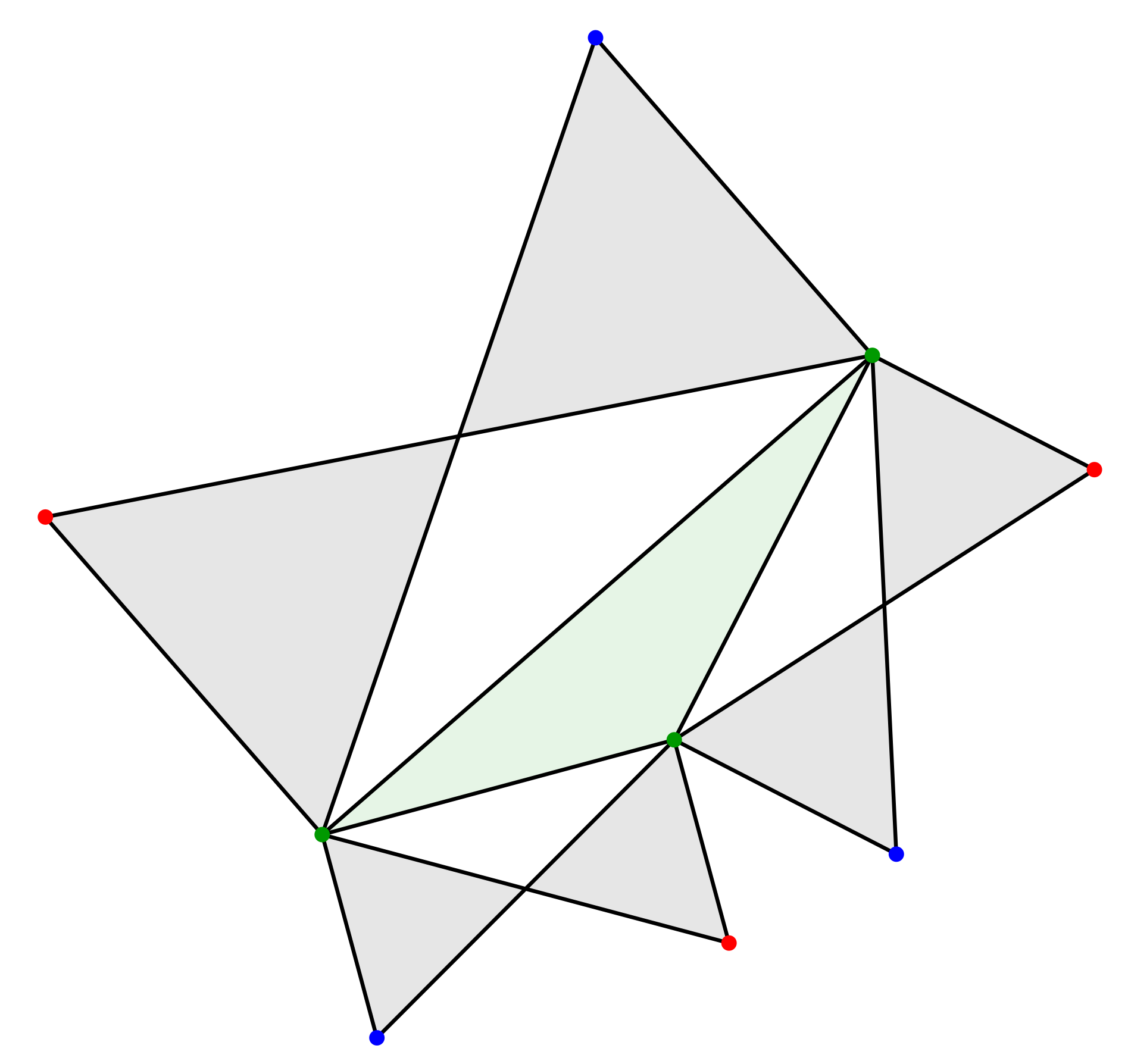
Abb. 1: Dreimal zwei gleichseitige Dreiecke

Die blauen Eckpunkte verbinden wir zu einem Dreieck (Abb. 2).

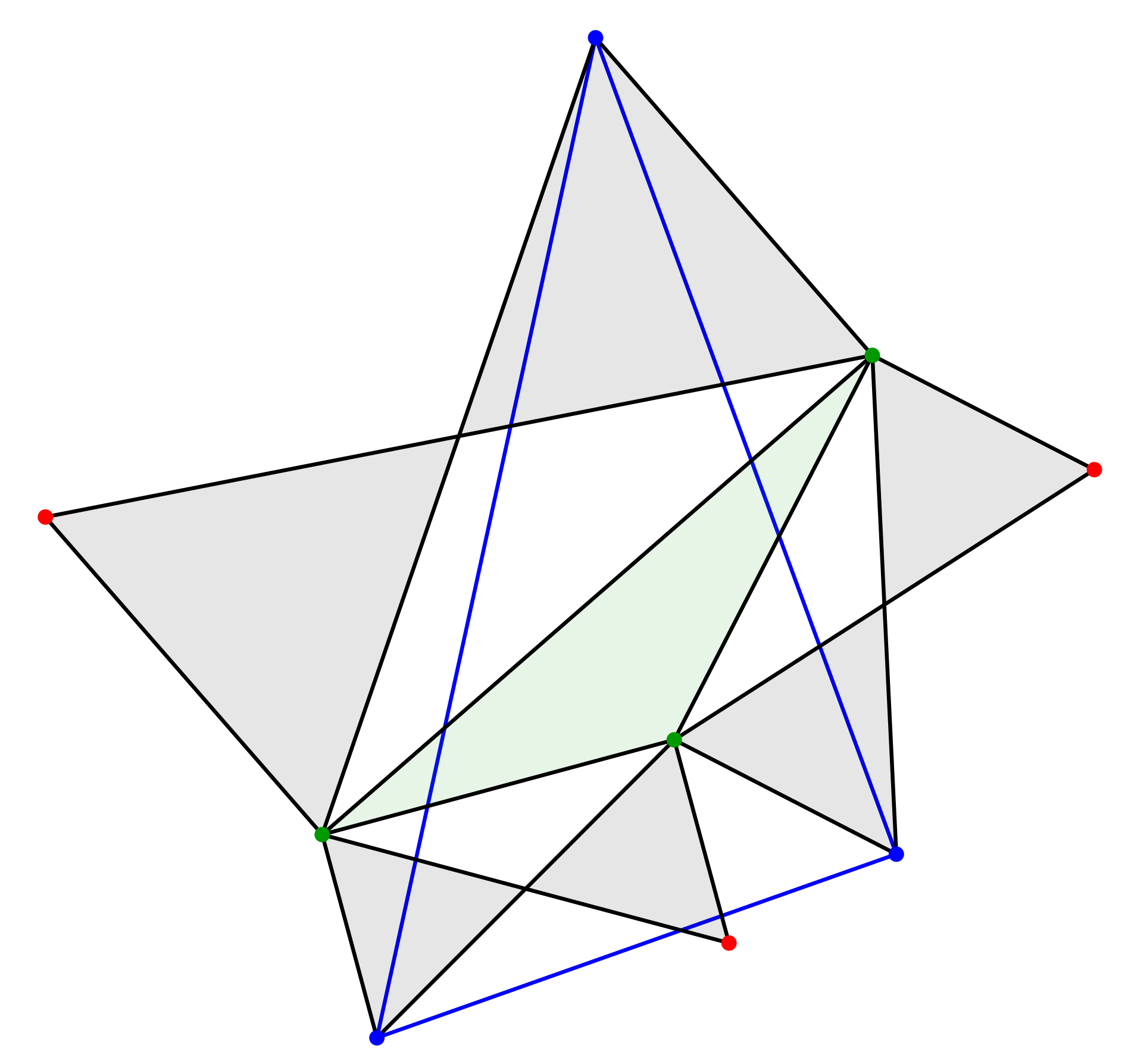
Abb. 2: Blaues Dreieck

Analog verbinden wir die roten Eckpunkte zu einem Dreieck (Abb. 3).

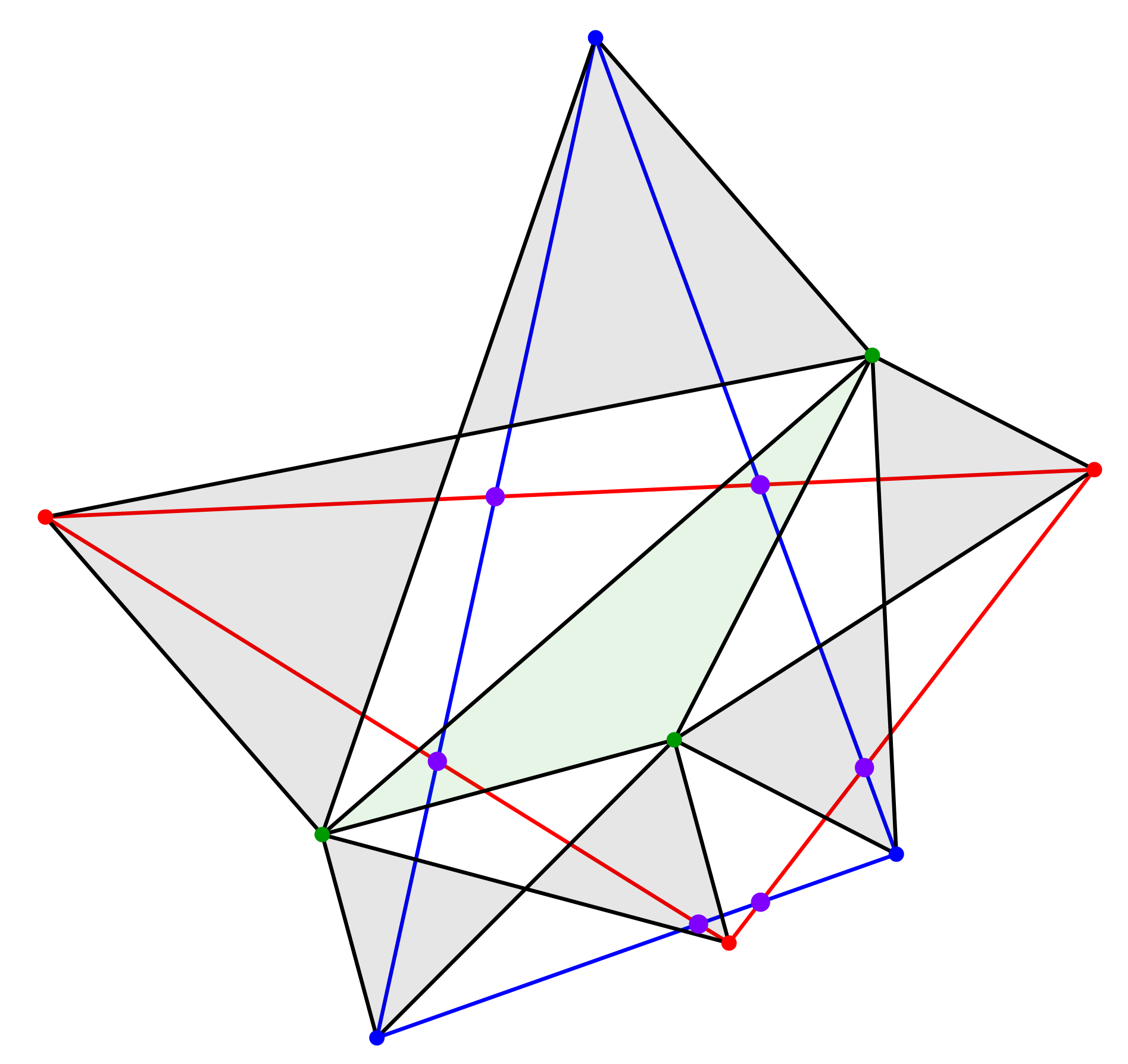
Abb. 3: Rotes Dreieck

Die beiden Dreiecke haben sechs Punkte gemeinsam. Diese liegen auf einer Ellipse (Abb. 4).

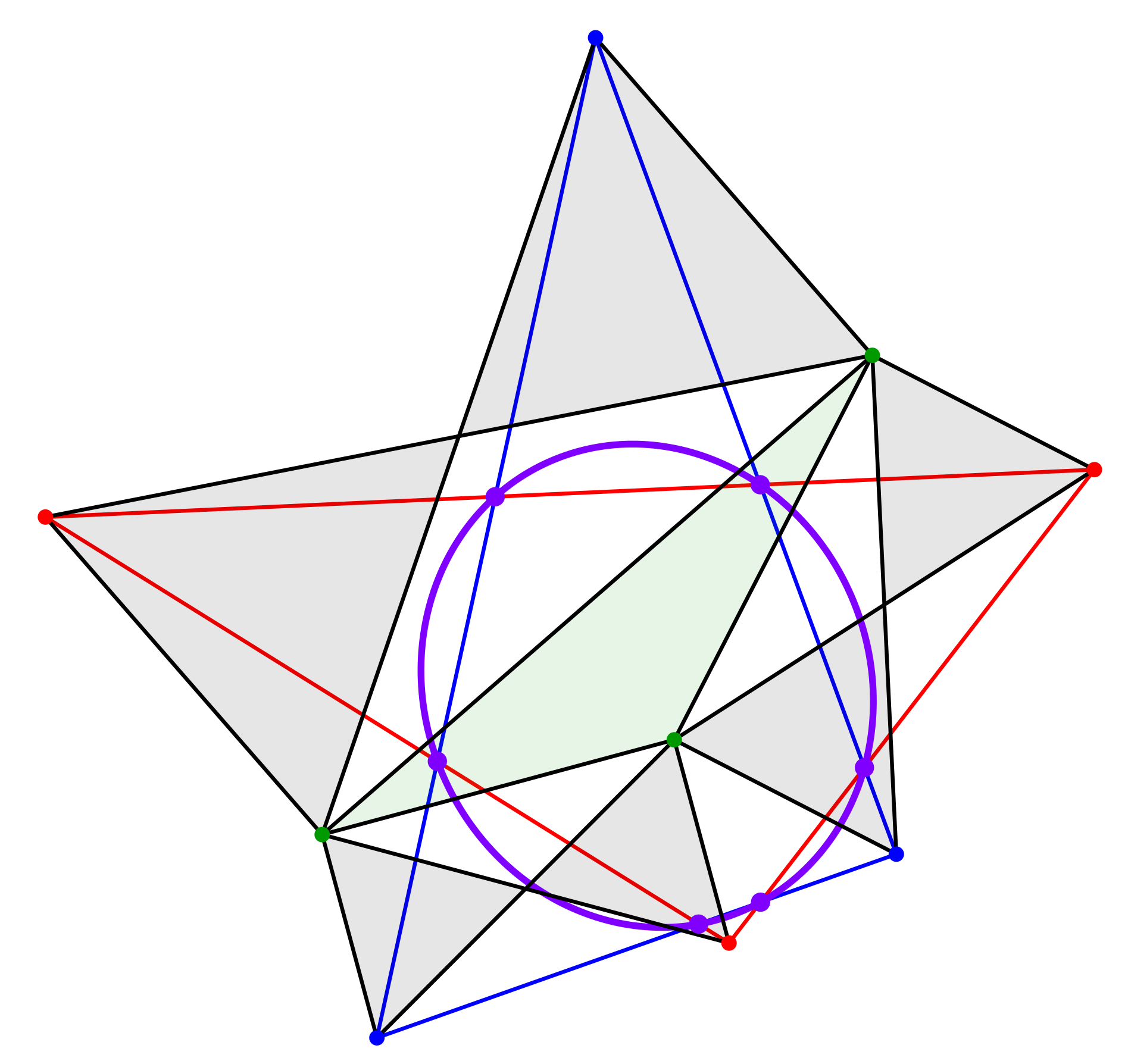
Abb. 4: Ellipse

Die gleichseitigen Dreiecke sind wesentlich. Wenn wir sie zum Beispiel durch rechtwinklig gleichschenklige Dreiecke ersetzen (Abb. 5), definieren fünf Schnittpunkte zwar eine Ellipse, aber der sechste liegt nicht darauf.

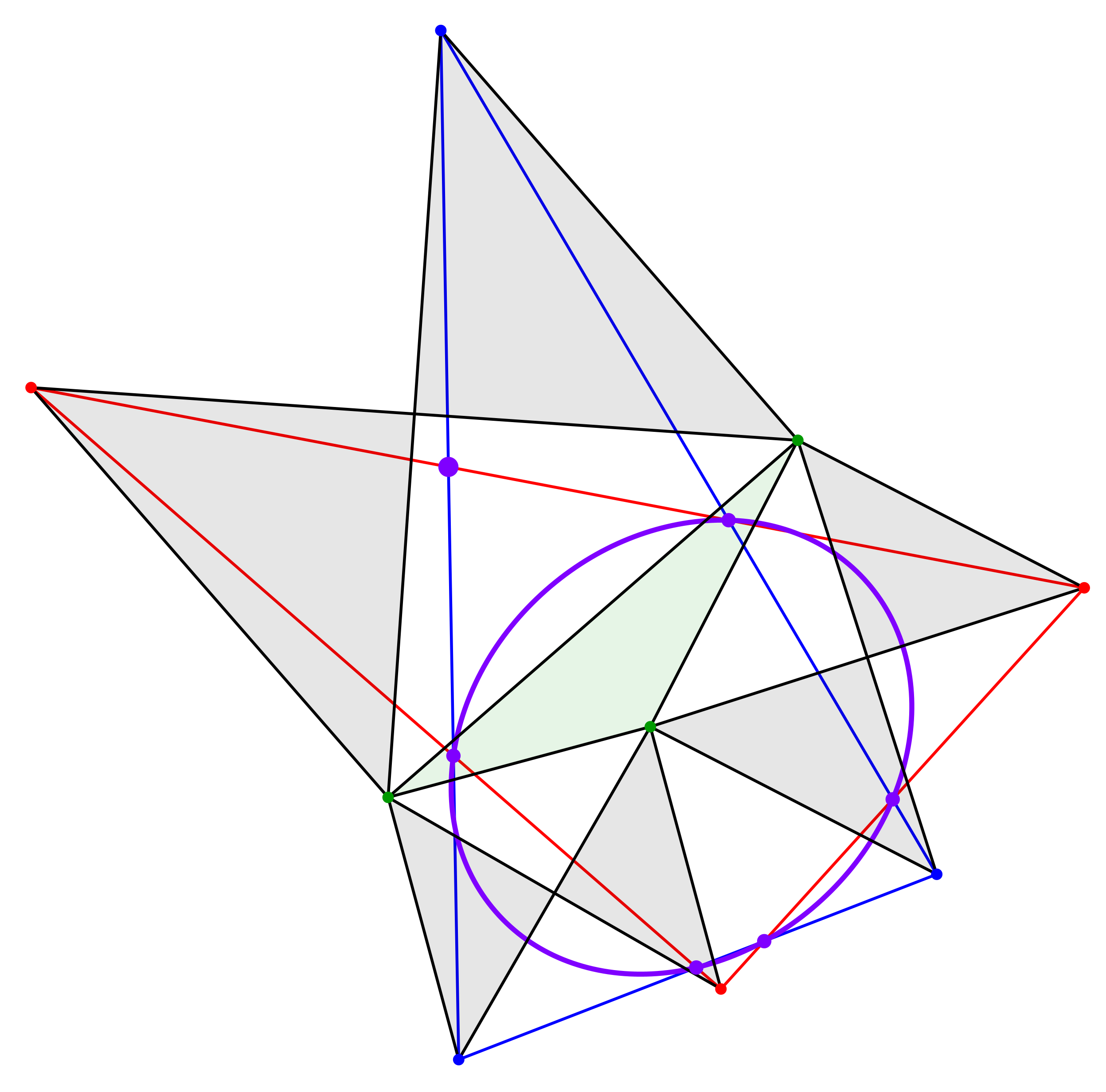
Abb. 5: Gegenbeispiel