Hans Walser, [20220104]
Ellipsen-Spiralen
1 Worum geht es?
Spielerei mit Ellipsen in mehreren Farben. Logarithmische Spiralen
2 Ellipsen-Trikolore
2.1 Gleiche Flächenanteile
Wir beginnen mit einer Ellipse mit dem Achsenverhältnis sqrt(3):1. Diese Ellipse malen wir in der linken Hälfte blau, in der rechten Hälfte rot aus (Abb. 1a). Nun sparen wir in der Mitte eine zur Ausgangsellipse ähnliche, aber senkrecht stehende weiße Ellipse aus (Abb. 1b). Dadurch entsteht eine Ellipsen-Trikolore. Wegen dem Achsenverhältnis sqrt(3):1 sind die drei Flächenanteile gleich groß.

Abb. 1: Ellipsen-Trikolore
2.2 Ungleiche Flächenanteile
Bei anderen Achsenverhältnissen ändern auch die Flächenanteile. Das Achsenverhältnis sqrt(2):1 (Abb. 2a) führt zur Flächenverteilung 1:2:1. Beim Achsenverhältnis 2:1 ergibt sich die Flächenverteilung 3:2:3 (Abb. 2b). Bei sqrt(5) erhalten wir 2:1:2 (Abb. 2c).
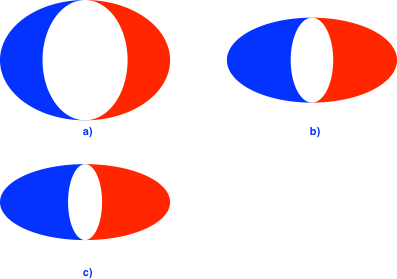
Abb. 2: Andere Flächenanteile
Allgemein erhalten wir beim Achsenverhältnis sqrt(n) die Farbverteilung (n–1):(2n):(n–1).
Natürlich geht es auch mit fünf Farben mit Gleichverteilung (Abb. 3).

Abb. 3: Fünf Farben
3 Spiralen
In die Figur der Abbildung 1b passen wir mittig eine verkleinerte und um 90° verdrehte Kopie der Gesamtfigur ein (Abb. 4a). Durch Iteration (Abb. 4b) erhalten wir schließlich zwei ineinanderlaufende Spiralen (Abb. 4c). Der weiße Anteil ist nun verschwunden. Die Spiralen sind vom logarithmischen Typ.

Abb. 4: Aufbau der Spirale
Die Abbildung 5 zeigt die der Abbildung 2 entsprechenden Spiralen.

Abb. 5: Spiralen
Die Abbildung 6 zeigt die Spirale, basierend auf der Ellipse mit den fünf Farben (Abb. 3). Man hat etwas Mühe, die Spiralen zu sehen.

Abb. 6: Fünf Farben
4 Unrund
Mit dem Achsenverhältnis sqrt(1.1):1 entsteht fast ein Kreis (Abb. 7a und 7b). In der Abbildung 7c sind 50 Iterationsschritte gezeichnet.
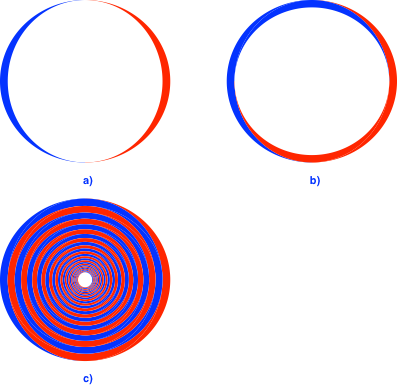
Abb. 7: Fast ein Kreis
Dass die Sache nicht rund ist, wird beim Drehen offensichtlich.
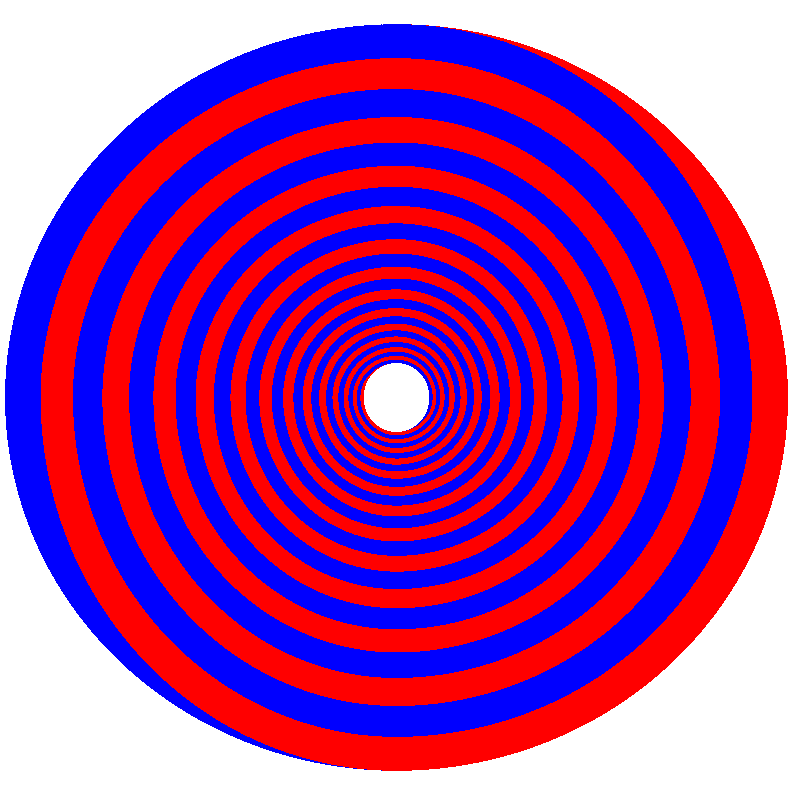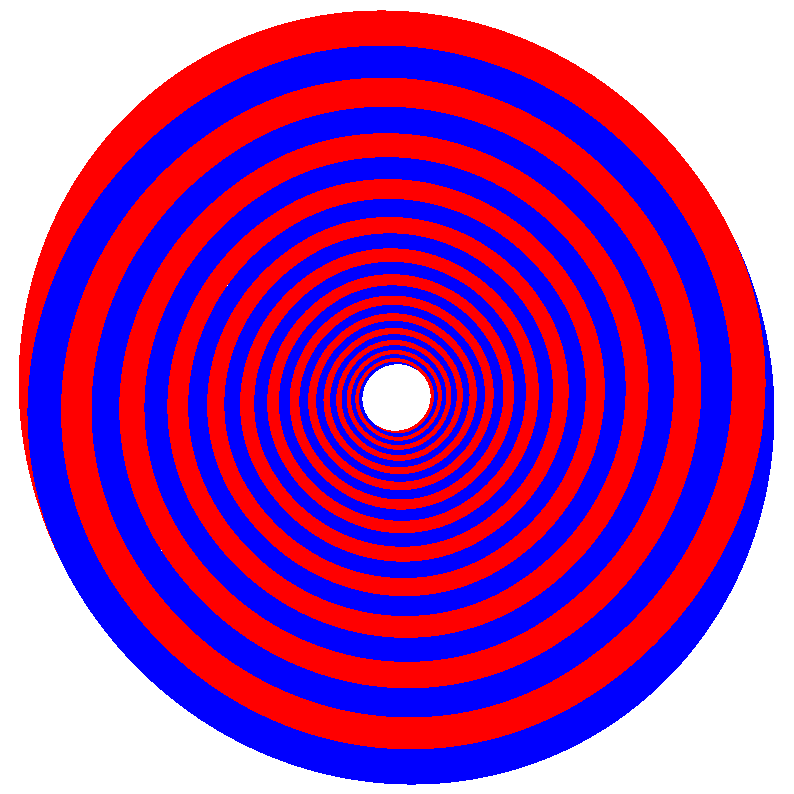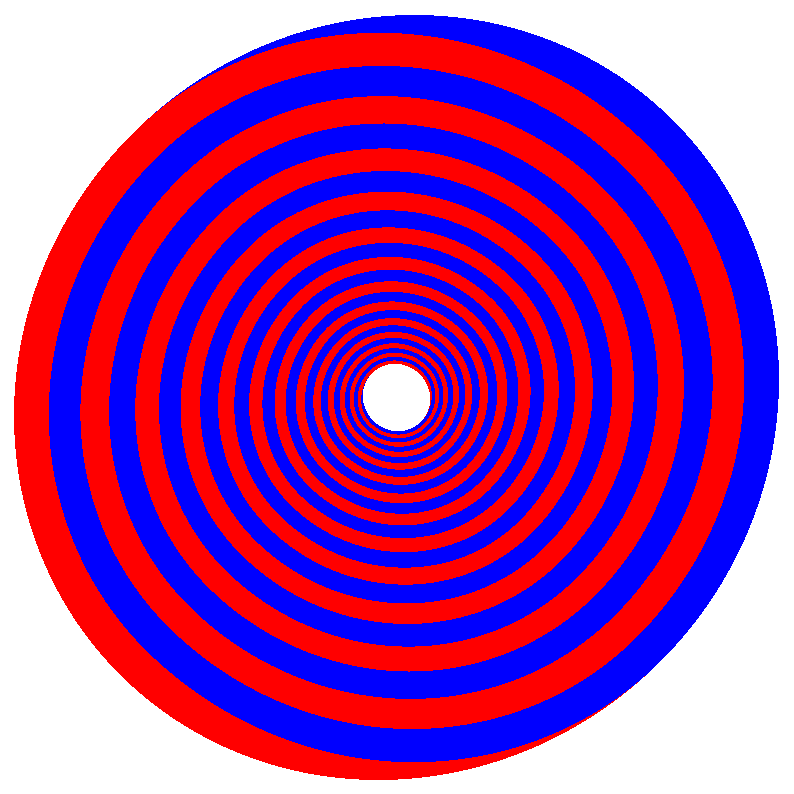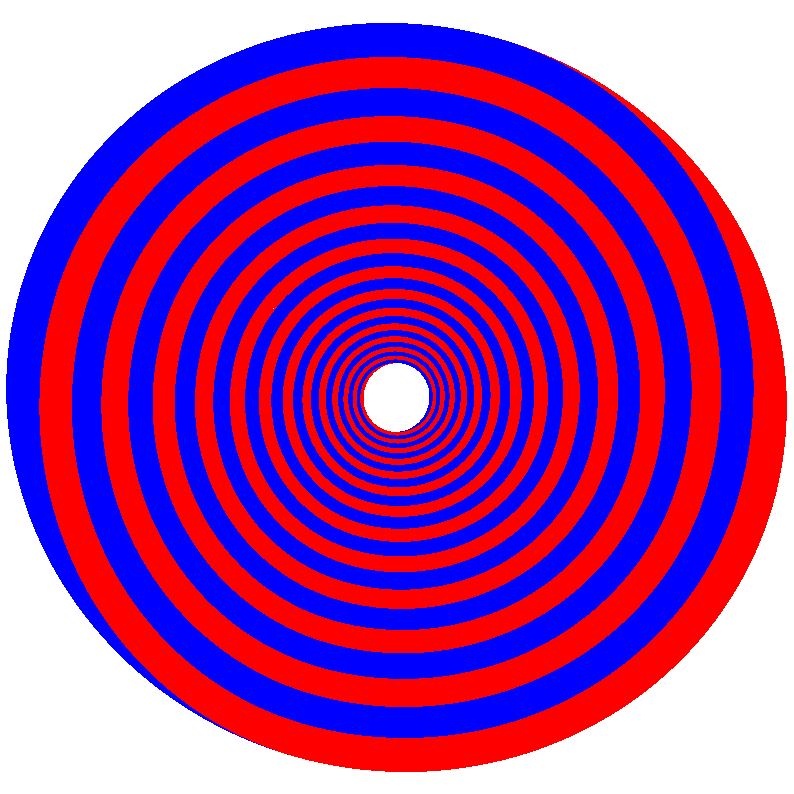
Abb. 8: Drehen
Websites
Hans Walser: Trikolore-Spiralen
http://www.walser-h-m.ch/hans/Miniaturen/T/Trikolore-Spiralen/Trikolore-Spiralen.html
Hans Walser: Cantor-Trikolore
http://www.walser-h-m.ch/hans/Miniaturen/C/Cantor-Trikolore/Cantor-Trikolore.htm
Hans Walser: Cantor-Bicolore
http://www.walser-h-m.ch/hans/Miniaturen/C/Cantor-Bikolore/Cantor-Bikolore.htm