Hans Walser, [20180711]
Ellipsen in Ellipse
1 Die Figur
Wir suchen Ellipsen mit folgender Eigenschaft.
Wir stellen n solcher Ellipsen im Hochformat nebeneinander (Abb. 1 fźr n = 4). Dann sollen sie in eine formgleiche grš§ere Ellipse im Querformat passen derart, dass die Krźmmungskreise in den stumpfen Scheiteln der stehenden kleinen Ellipsen mit den Krźmmungskreisen in den spitzen Scheiteln der liegenden gro§en Ellipse źbereinstimmen. Wir haben also links und rechts au§en nicht nur eine Berźhrung, sondern einen kissing point.
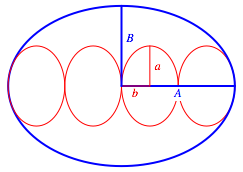
Abb. 1: Aufgabenstellung und Bezeichnungen
2 Berechnungen
Die kleinen Ellipsen haben die Halbachsen a und b, die gro§e Ellipse die Halbachsen A und B.
Der Krźmmungskreisradius r in einem stumpfen Scheitel der kleinen Ellipsen ist:
![]() (1)
(1)
Der Krźmmungskreisradius R in einem spitzen Scheitel der gro§en Ellipse ist:
![]() (2)
(2)
Die kissing point Bedingung fźhrt auf:
![]() (3)
(3)
Die €hnlichkeit der kleinen Ellipsen mit der gro§en Ellipse bedeutet:
![]() (4)
(4)
Weiter ist als Folge des Nebeneinanderstellens der kleinen Ellipsen:
![]() (5)
(5)
Wir fźhren eine Normierung fźr b ein:
![]() (6)
(6)
Aus den Gleichungen (3) bis (6) ergibt sich:
![]() (7)
(7)
3 Beispiele
3.1 Eine kleine Ellipse
Die kleine und die gro§e Ellipse sind beide der Einheitskreis (Abb. 2.1).

Abb. 2.1: Kreis im Kreis
3.2 Zwei kleine Ellipsen

Abb. 2.2: Zwei kleine Ellipsen
Die Figur kann (wie auch alle folgenden Figuren) fraktalisiert werden (Abb. 2.2a)
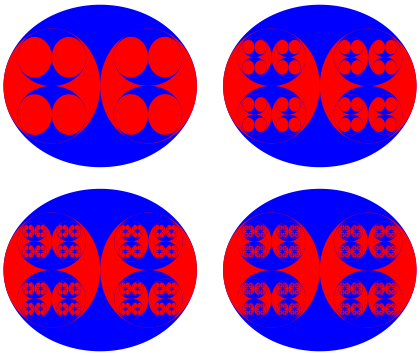
Abb. 2.2a: Entstehung des Fraktals
3.3 Drei kleine Ellipsen
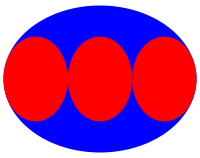
Abb. 2.3: Drei kleine Ellipsen
3.4 Vier kleine Ellipsen
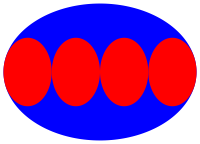
Abb. 2.4: Vier kleine Ellipsen
Die Ellipsen passen in ein Rechteck im DIN-Format (Abb. 2.4a) [1] .
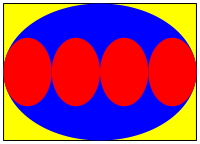
Abb. 2.4a: Einpassen in ein DIN-Rechteck
3.5 Fźnf kleine Ellipsen
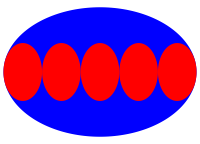
Abb. 2.5: Fźnf kleine Ellipsen
3.6 Sechs kleine Ellipsen
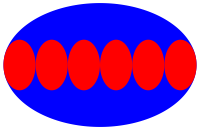
Abb. 2.6: Sechs kleine Ellipsen
3.7 Sieben kleine Ellipsen

Abb. 2.7: Sieben kleine Ellipsen
3.8 Acht kleine Ellipsen
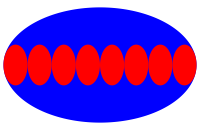
Abb. 2.8: Acht kleine Ellipsen
3.9 Neun kleine Ellipsen
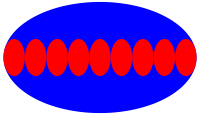
Abb. 2.9: Neun kleine Ellipsen
Wir kšnnen noch weitere stehende kleine Ellipsen einfźgen (Abb. 2.9a).

Abb. 2.9a: Noch zwei Ellipsen
Die Figur lŠsst sich in ein regulŠres Dreiecksraster einpassen (Abb. 2.9b).

Abb. 2.9b: RegulŠres Dreiecksraster
Die Abbildung 3 zeigt eine †berlagerung der Abbildungen 2.1 bis 2.9.

Abb. 3: †berlagerung
Die †berlagerung ist allerdings nicht ma§stŠblich. Es wurden alle Abbildungen auf die gleiche Breite skaliert. Die optischen Effekte sind eine Folge der unterschiedlichen Skalierungen.
Die Abbildung 4 zeigt dagegen eine ma§stŠbliche †berlagerung der Abbildungen 2.1 bis 2.9.

Abb. 4: Ma§stŠbliche †berlagerung
Websites
[1] Hans Walser: Ellipsen im DIN-Format:
http://www.walser-h-m.ch/hans/Miniaturen/E/Ellipsen_DIN/Ellipsen_DIN.htm