Hans Walser, [20180712]
Ellipsenfraktal
1 Konstruktion
Wir beginnen mit einer liegenden Ellipse mit den Achsen a und b (Abb. 1a):
![]() (1)
(1)
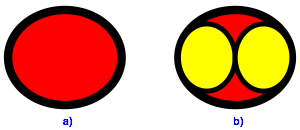
Abb. 1: Start und erster Schritt
Davon machen wir zwei Kopien (gelb in Abb. 1b) mit dem Verkleinerungsfaktor r:
![]() (2)
(2)
Diese stellen wir hochkant und platzieren sie gemŠ§ Abbildung 1b in die rote Ellipse. Die gelben Ellipsen berźhren einander in einem stumpfen Scheitel und haben links und rechts au§en in den Berźhrungspunkten mit der roten Ellipse denselben Krźmmungskreis wie die rote Ellipse. Wir haben eine kissing point Situation. Die gelben Ellipsen schmiegen sich bestmšglich an die rote.
Rechnerische Herleitung siehe [1].
Nun iterieren wir den Prozess. Die Abbildungen 2 und 3 zeigen die Folgeschritte.
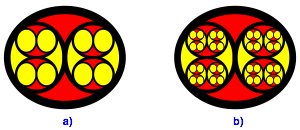
Abb. 2: Folgeschritte
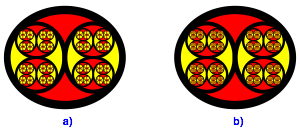
Abb. 3: Folgeschritte
Wenn wir immer so weiterfahren, erhalten wir das Fraktal. Da wir aber nicht unendlich lang leben und auch die SpeicherkapazitŠt meines Computers beschrŠnkt ist, mźssen wir mit den vorlŠufigen Bildern vorlieb nehmen.
2 Beispiele
Die folgenden Abbildungen zeigen grafische Varianten der Abbildung 3b.
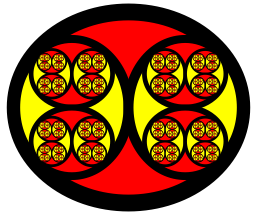
Abb. 4: Zweifarbig, schwarze Linien
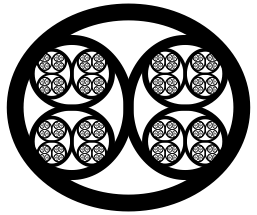
Abb. 5: Linien

Abb. 6: Zweifarbig, wei§e Linien

Abb. 7: Zweifarbig

Abb. 8: Einfarbig, wei§e Linien
3 Fraktale Dimension
Die fraktale Dimension D (Mandelbrot Dimension) ist:
![]() (3)
(3)
Wir haben in unserem Beispiel eine rationale fraktale Dimension.
4 Variante
Die Abbildungen 9, 10 und 11 zeigen eine Variante. Rechnerische Herleitung siehe [1].
Auch
diese Variante hat die fraktale Dimension ![]() .
.
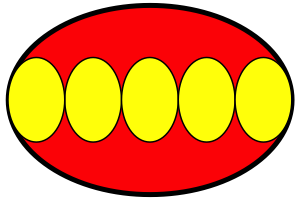
Abb. 9: Variante mit fźnf kleinen Ellipsen
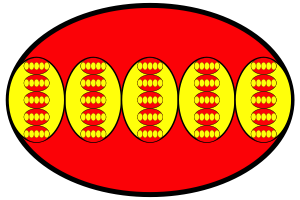
Abb. 10: Iteration
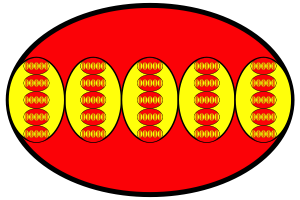
Abb. 11: Weitere Iteration
Weblinks
[1] Hans Walser: Ellipsen in Ellipse (11.07.2018):
www.walser-h-m.ch/hans/Miniaturen/E/Ellipsen_in_Ellipse/Ellipsen_in_Ellipse.htm
Literatur
Mandelbrot, Beno”t B. (1983). The Fractal Geometry of Nature. New York: Freeman. ISBN 0-7167-1186-9
Mandelbrot, Beno”t B. (1991). Die fraktale Geometrie der Natur. Basel: BirkhŠuser.