Hans Walser, [20201009]

Ellipsenspielerei

Anregung: Zvonimir Durcevic, Wien

In einem beliebigen Ellipsenpunkt A zeichnen wir die Normale (Abb. 1.1).

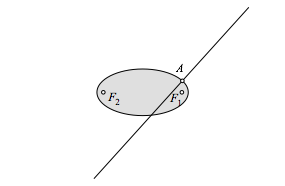
Abb. 1.1: Ellipsennormale

Diese Normale hat einen zweiten Schnittpunkt B mit der Ellipse (Abb. 1.2)

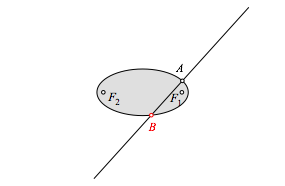
Abb. 1.2. Zweiter Schnittpunkt

Wir spiegeln B an A und erhalten so C. Bei Variation von A beschreibt C die rote Kurve (Abb. 1.3). Der Autor weiß nicht, was das für eine Kurve ist.

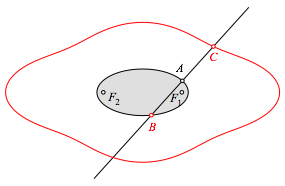
Abb. 1.3: Bahnkurve von C

Nun spiegeln wir noch A an B und erhalten mit dem Spiegelpunkt D die blaue Kurve der Abbildung 1.4.

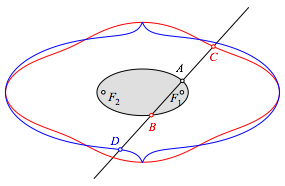
Abb. 1.4: Bahnkurve von D

Die Form dieser Kurven hängt von der Form der Ellipse ab. Wir lassen nun die lange Ellipsenachse fest, variieren aber die beiden Brennpunkte F₁ und F₂ (Animation 1).

Animation 1: Variation der Ellipsenform