Hans Walser, [20201006]

Ellipsentangente und Herzkurve

Idee und Anregung: Zvonimir Durcevic, Wien

1 Problemstellung

Von einer Ellipse kennen wir die beiden Brennpunkte und die lange Achse (Abb. 1). Gesucht ist eine Ellipsentangente mit vorgegebener Richtung.

Abb. 1: Lange Achse und Brennpunkte

2 Konstruktion der Ellipsentangente

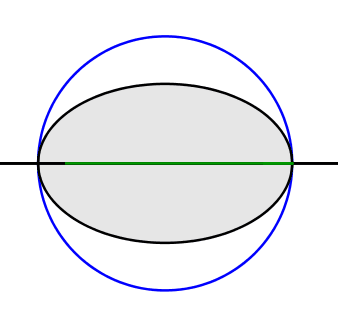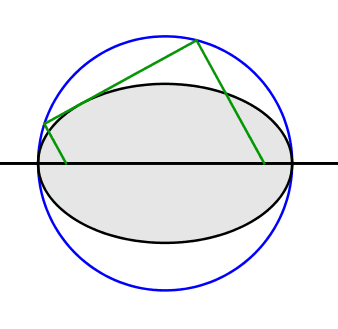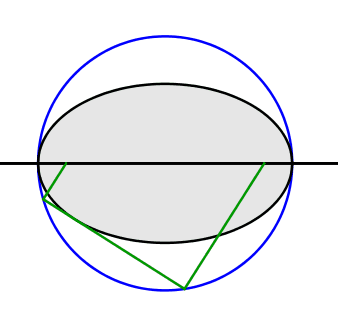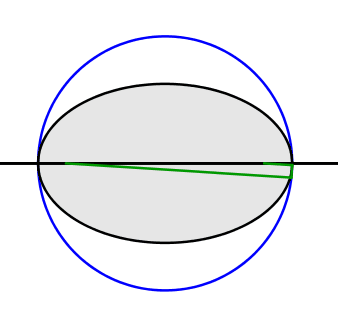
Wir zeichnen den Thaleskreis über der langen Achse (Abb. 2.1)

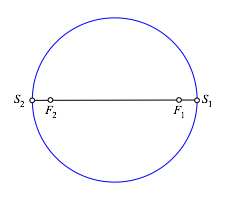
Abb. 2.1: Thaleskreis

Durch die beiden Brennpunkte zeichnen wir zwei parallele Strahlen, welche orthogonal zur vorgegebenen Tangentenrichtung sind. Diese Strahlen schneiden wir mit dem Thaleskreis (Abb. 2.2).

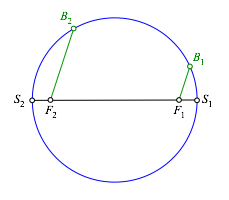
Abb. 2.2: Parallele Strahlen

Die Verbindung der beiden Schnittpunkte (Abb. 2.3) ist orthogonal zu den beiden Strahlen. Wir haben es also hier mit einer Verallgemeinerung des Thaleskreis-Begriffes zu tun.

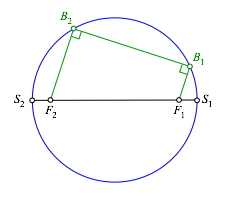
Abb. 2.3: Rechte Winkel

Diese Verbindung ist auch die gesuchte Tangente (Abb. 2.4).

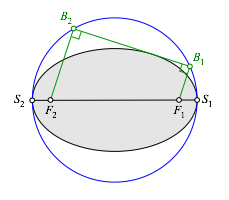
Abb. 2.4: Ellipsentangente

Interessant ist, dass wir vorerst keine Information über den Berührungspunkt haben.

Die Animation 1 zeigt den Sachverhalt.

Animation 1: Ellipsentangenten

Für die Hyperbel geht die Tangentenkonstruktion analog.

3 Berührungspunkt

Den Berührungspunkt B erhalten wir nun wie folgt. Wir spiegeln den einen Brennpunkt F₁ an B₁ (Abb. 3.1).

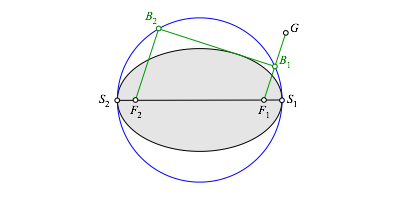
Abb. 3.1: Spiegelung des einen Brennpunktes

Den Spiegelpunkt G verbinden wir mit dem anderen Brennpunkt F₂. Der Schnittpunkt mit der Tangente ist der Berührungspunkt B (Abb. 3.2).

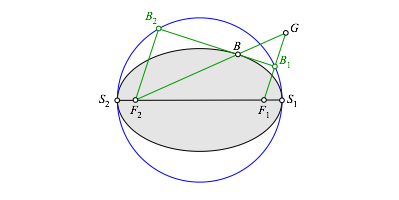
Abb. 3.2: Berührungspunkt

4 Eine Herzkurve

Wir spiegeln den Berührungspunkt B an B₁. Der Spiegelpunkt C beschreibt beim Abwälzen der Ellipsentangente eine Herzkurve (Abb. 4.1). Es handelt sich dabei allerdings nicht um die bekannte Kardioide.

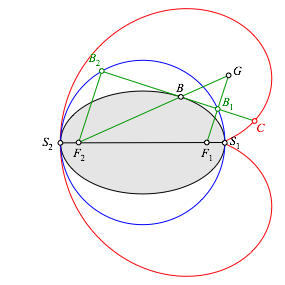
Abb. 4.1: Herzkurve

Das Viereck BF₁CG ist ein Rhombus (Abb. 4.2)

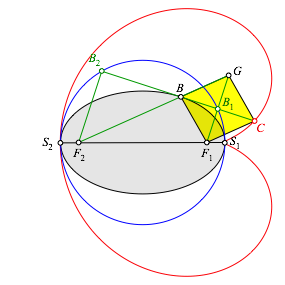
Abb. 4.2: Rhombus

Die Animation 2 beschreibt den Sachverhalt.

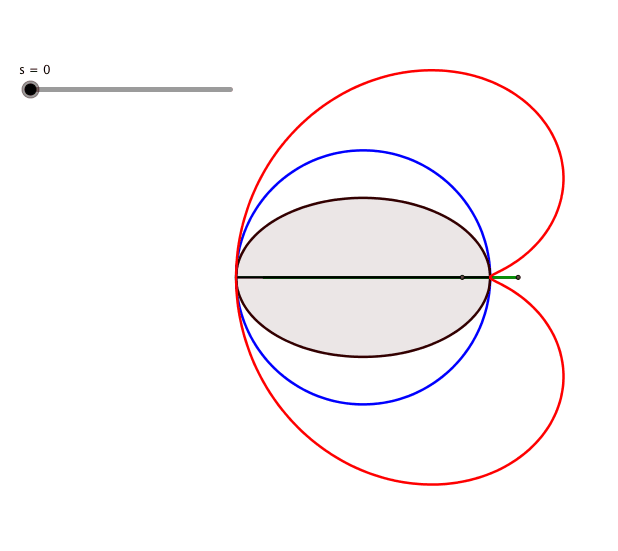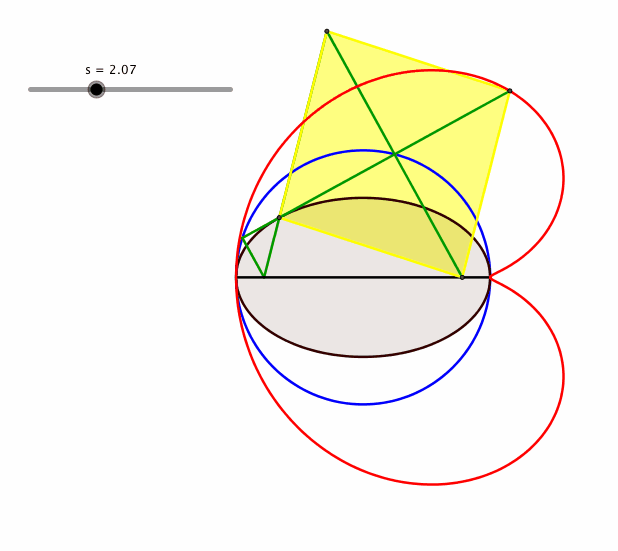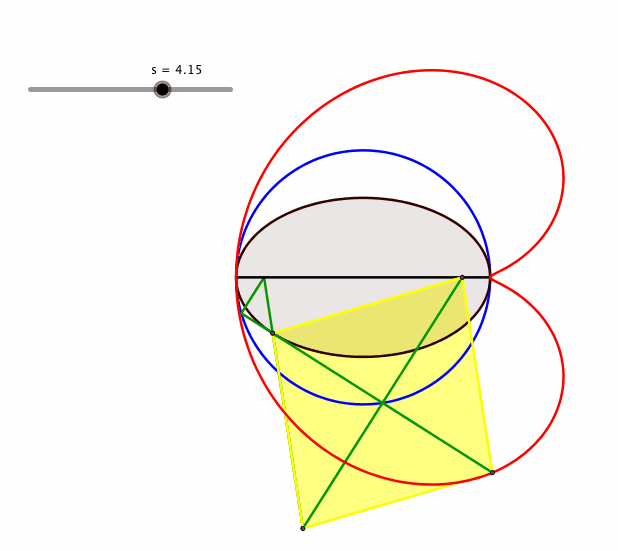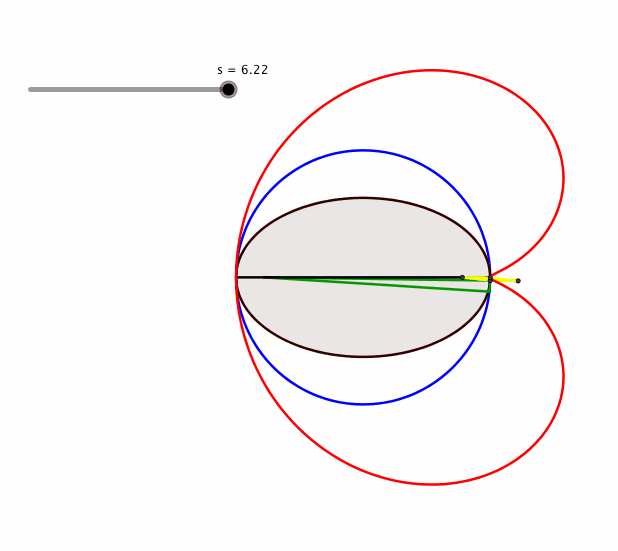
Animation 2: Herzkurve

Die Form der Herzkurve hängt von der Wahl der Brennpunkte ab (Animation 3). Bei Brennpunkten außerhalb des blauen Kreises haben wir anstelle der Ellipse eine Hyperbel. Die rote Kurve ist nicht mehr herzförmig.

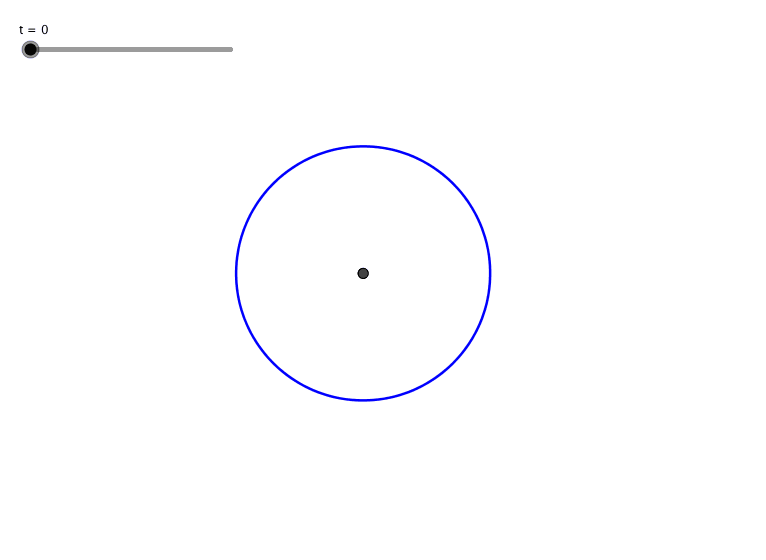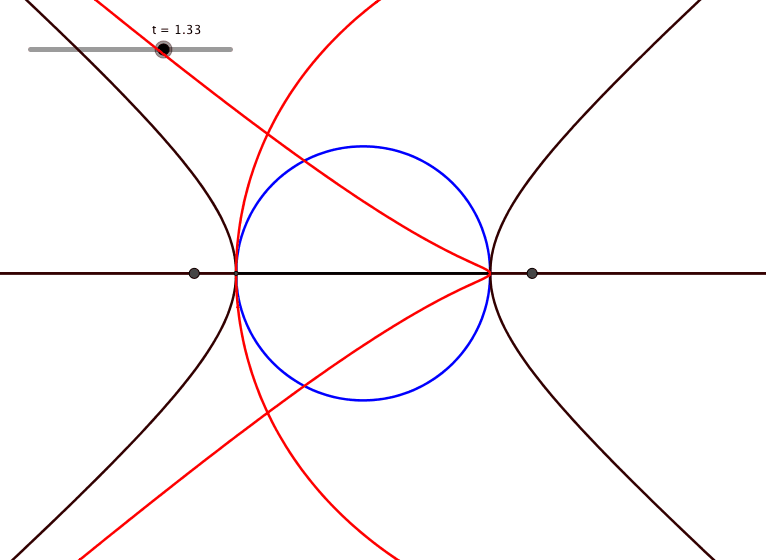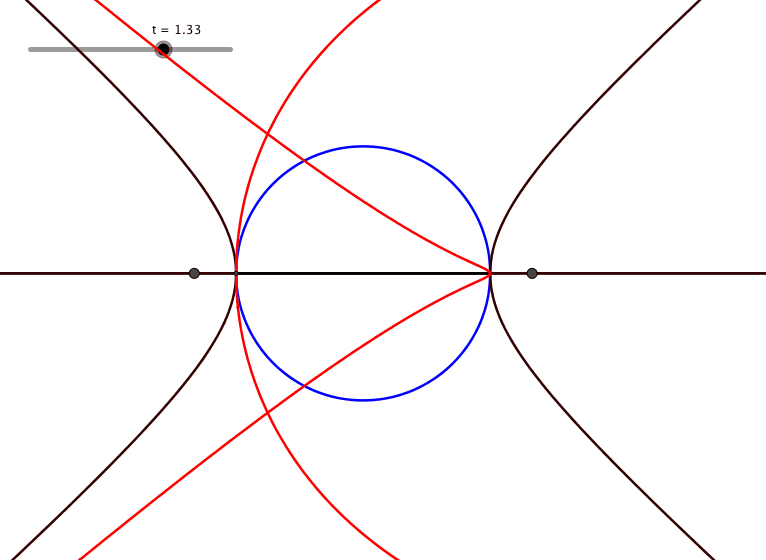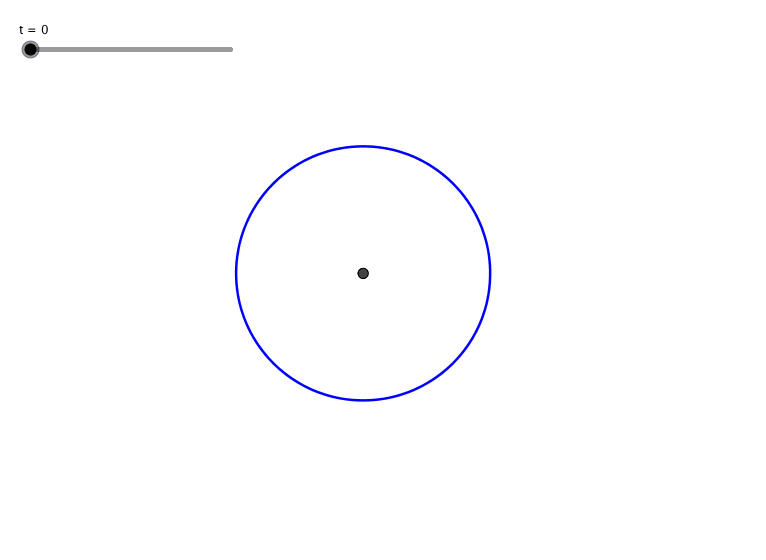
Animation 3: Brennpunkte und Form der Herzkurve

Websites

Hans Walser: Kegelschnitte und Thaleskreise

http://www.walser-h-m.ch/hans/Miniaturen/K/Kegelschnitte_u_Thaleskreise/Kegelschnitte_u_Thaleskreise.htm