Hans Walser, [20160530]
Epstein-Nielsen-Zerlegungsbeweis fźr den Satz des Pythagoras
Paul Epstein (1871-1939), Jakob Nielsen (1890-1959)
1 Klassisch
Die Abbildung 1 zeigt die klassische Version. Das Konstruktionsverfahren ergibt sich unmittelbar aus der Figur.
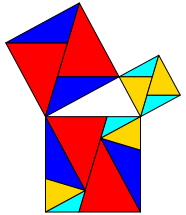
Abb. 1: Zerlegungsbeweis
2 Varianten
2.1 Andere Anordnung
Die Abbildung 2 zeigt eine Anordnungsvariante.
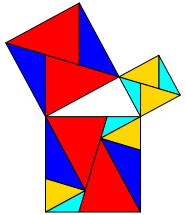
Abb. 2: Andere Anordnung
Die Abbildung 3 zeigt eine weitere Anordnungsvariante.
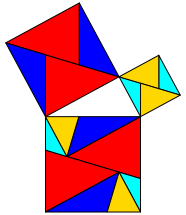
Abb. 3: Noch eine Anordnungsvariante
2.2 Trapeze
Wir setzen nur halbe Quadrate in Form von Trapezen an (Abb. 4).
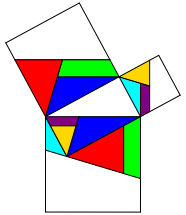
Abb. 4: Trapeze ansetzen
2.3 Rechtwinklig gleichschenklige Dreiecke
Wir arbeiten mit rechtwinklig gleichschenkligen Dreiecken (Abb. 5).
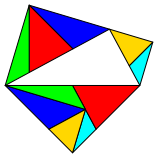
Abb. 5: Rechtwinklig gleichschenklige Dreiecke
Die Abbildung 6 gibt Hinweise fźr das Konstruktionsverfahren.
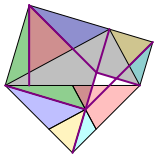
Abb. 6: Konstruktionsverfahren
Die Abbildung 7 zeigt eine symmetriesierte Version.
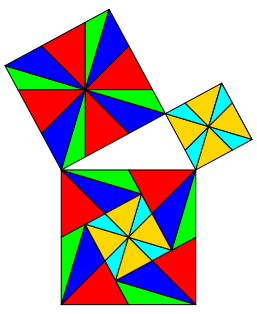
Abb. 7: Mehr Symmetrie
Das kann allerdings einfacher gestaltet werden (Abb. 8), und dann sind wir bei einem alten Bekannten.
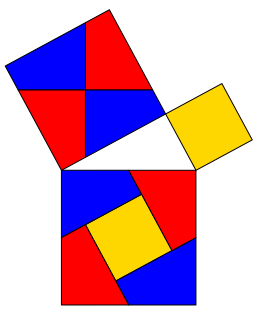
Abb. 8: Einfachere Gestaltung