Hans Walser, [20180701]
ErgŠnzung zum Rechteck
1 Worum geht es?
Spiel mit Tangenten und Rechtecken bei Kegelschnitten. Als Sonderfall erscheint das Rechteck im DIN-Format.
2 Parabel
Wir beginnen mit der Parabel (Abb. 1):
![]() (1)
(1)
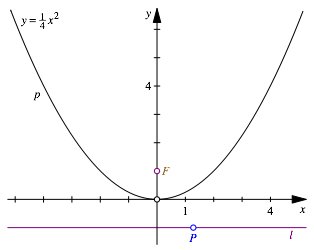
Abb. 1: Parabel mit Brennpunkt und Leitlinie
Die
Parabel p hat den Brennpunkt ![]() und die Leitlinie
und die Leitlinie ![]() . Auf der Leitlinie l wŠhlen wir einen Punkt P.
. Auf der Leitlinie l wŠhlen wir einen Punkt P.
2.1 Tangenten und Rechteck
Die Tangenten von P an die Parabel p sind orthogonal (Abb. 2). Die Berźhrungspunkte bezeichnen wir mit B1 und B2.
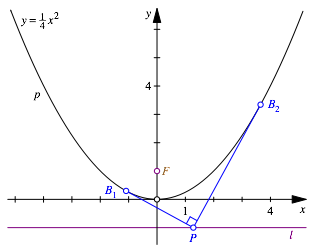
Abb. 2: Tangenten
Wir ergŠnzen das rechtwinklige Dreieck B2B1P zum Rechteck B2SB1P (Abb. 3).
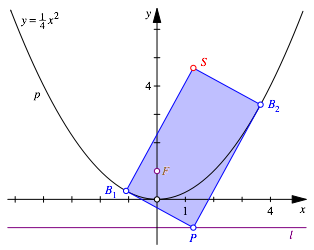
Abb. 3: ErgŠnzung zum Rechteck
Die Frage ist nun, welche Kurve der Punkt S beschreibt, wenn P auf l variiert.
Wir erhalten wieder eine Parabel (Abb. 4).
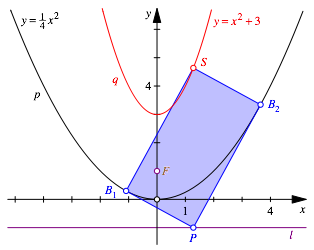
Abb. 4: Zweite Parabel
Diese Parabel hat die Gleichung:
![]() (2)
(2)
Dies kann durch Rechnung nachgewiesen werden.
2.2 Scheitelkrźmmungskreise
Die
Scheitelkrźmmungskreise der beiden Parabeln haben den Punkt ![]() gemeinsam
(Abb. 5). Wir kšnnen die Parabel q
durch eine Streckung mit dem Zentrum Z
und dem Faktor 4 auf die Parabel p
abbilden.
gemeinsam
(Abb. 5). Wir kšnnen die Parabel q
durch eine Streckung mit dem Zentrum Z
und dem Faktor 4 auf die Parabel p
abbilden.
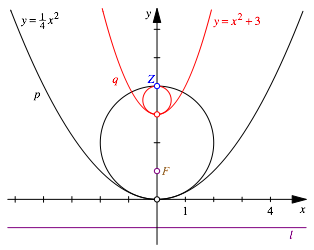
Abb. 5: Krźmmungskreise in den Scheiteln
2.3 SonderfŠlle
Im symmetrischen Fall ist das Rechteck ein auf der Spitze stehendes Quadrat (Abb. 6). Der Brennpunkt F ist das Zentrum des Quadrates.
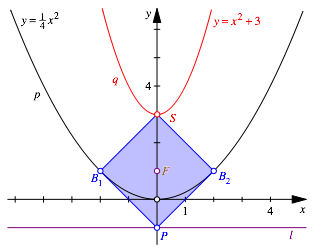
Abb. 6: Sonderfall Quadrat
Die Abbildung 7 zeigt einen interessanten Sonderfall: Die Rechteckseiten sind nicht nur tangential oder normal zur Parabel p sondern auch zur Parabel q.
Die
Oberkante B2S liegt auf einer Geraden durch Z. Das Rechteck hat das SeitenverhŠltnis ![]() , entspricht also dem DIN-Format (Walser 2013).
, entspricht also dem DIN-Format (Walser 2013).
Die Strecke B2S ist eine der beiden Minimaltransversalen (die andere liegt symmetrisch dazu) der beiden Parabeln. Sie hat die LŠnge:
![]() (3)
(3)
Eine Kreisscheibe mit dem Durchmesser dieser Strecke B2S ist die grš§te Kreisscheibe, die zwischen den beiden Parabeln durchgeschoben werden kann.
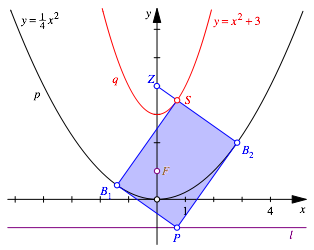
Abb. 7: DIN-Format
Die Figur kann iteriert werden (Abb. 8).
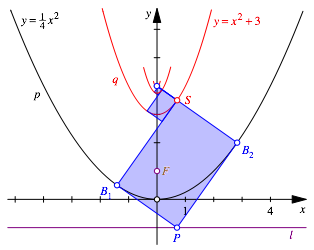
Abb. 8: Iteration
3 Ellipse
Die Punkte, von denen aus eine Ellipse (oder eine Hyperbel) unter einem rechten Winkel gesehen wird, bilden einen Kreis (ăThaleskreisŇ, [1] ). Bei einer Ellipse mit den Halbachsen a und b hat der Kreis den Radius r:
![]() (4)
(4)
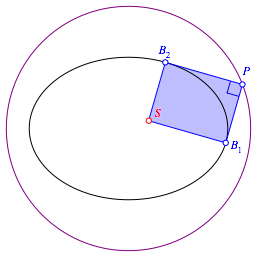
Abb. 9: Thaleskreis an die Ellipse
Die ergŠnzende Ecke S zeichnet eine Rosette (Abb. 10).
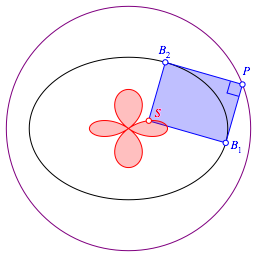
Abb. 10: Rosette
4 Hyperbel
Wir haben einen Thaleskreis (Abb. 11) mit dem Radius r
![]() (5)
(5)
Es muss also a ł b sein, damit man rechtwinklige Tangenten an die Hyperbel zeichnen kann.
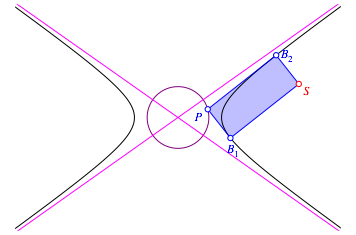
Abb. 11: Thaleskreis der Hyperbel
Der ergŠnzende Punkt S beschreibt eine aus vier €sten bestehende Kurve (Abb. 12).
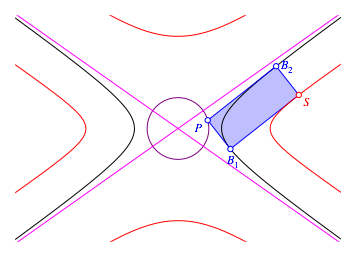
Abb. 12: Vierteilige Kurve
Websites
Hans Walser: Tangenten an Ellipse und Hyperbel (abgerufen 02.07.2018):
http://www.walser-h-m.ch/hans/Miniaturen/T/Tangenten_E_H/Tangenten_E_H
Literaturverzeichnis
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.