0 Worum geht es?

Relativität der Bahnkurven

1 Der Euklid-Punkt

Euklid (Euklid 1980, S. 32, Gerwig 2021, S. 20, 136, 319) illustriert den Beweis desjenigen Satzes, der heute als Satz von Pythagoras bezeichnet wird (Euklid verwendet diese Bezeichnung nicht), die Figur der Abbildung 1a (Nachzeichnung durch den Autor).

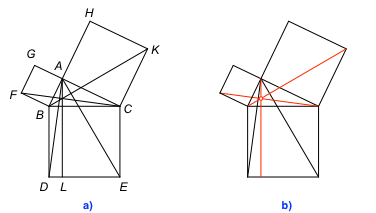
Abb. 1: Der Euklid-Punkt

Vermutung: Die drei rot markierten Geraden (Abb. 1b) haben einen gemeinsamen Schnittpunkt, den Euklid-Punkt.

2 Beweis

Die in der Abbildung 1b senkrecht eingezeichnete Gerade ist die Höhe des rechtwinkligen Dreieckes. Das Hypotenusenquadrat ist für die Beweisführung irrelevant und wird im Folgenden nicht gezeichnet.

Wir arbeiten mit der Disposition der Abbildung 2. Das rechtwinklige Dreieck habe die Katheten a und b.

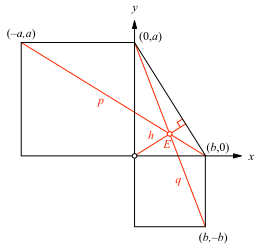
Abb. 2: Disposition

Für die drei Geraden h, p und q ergeben sich die Gleichungen:

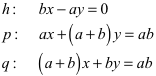(1)

Die Gleichung für h ist die Differenz der Gleichungen für q und für p. Sie ist also eine Linearkombination dieser beiden Gleichungen. Damit ist die Schnittpunkteigenschaft bewiesen. Für den Euklid-Punkt E erhalten wir:

(2)

3 Bahnkurven

3.1 Klassisch

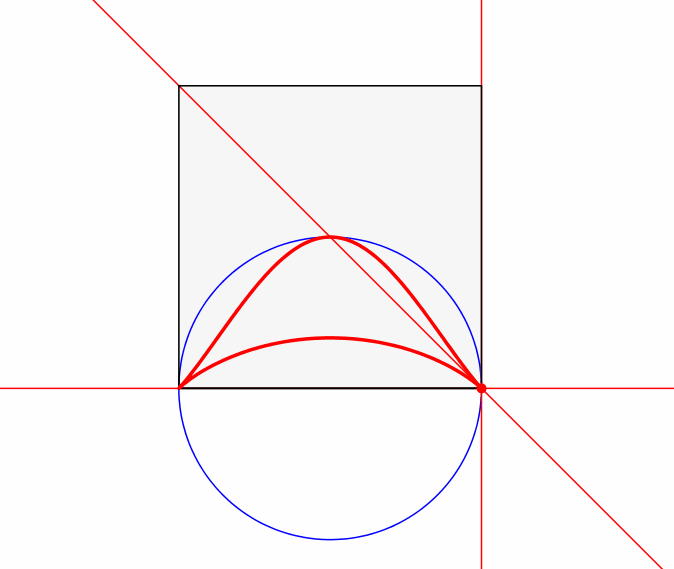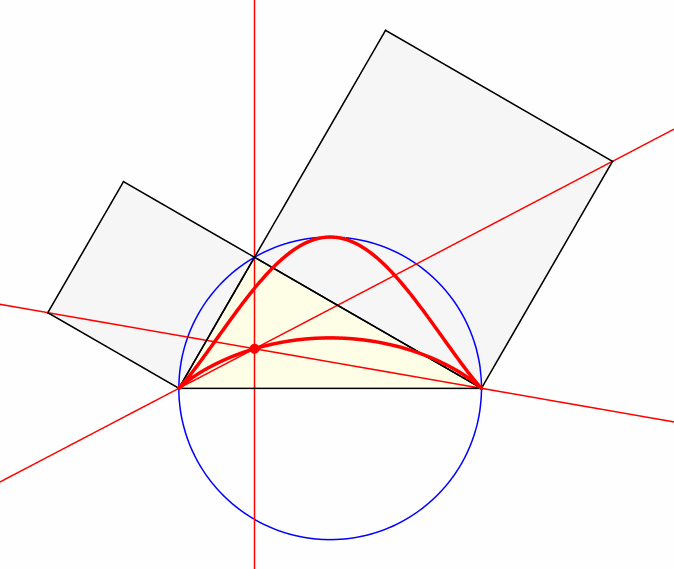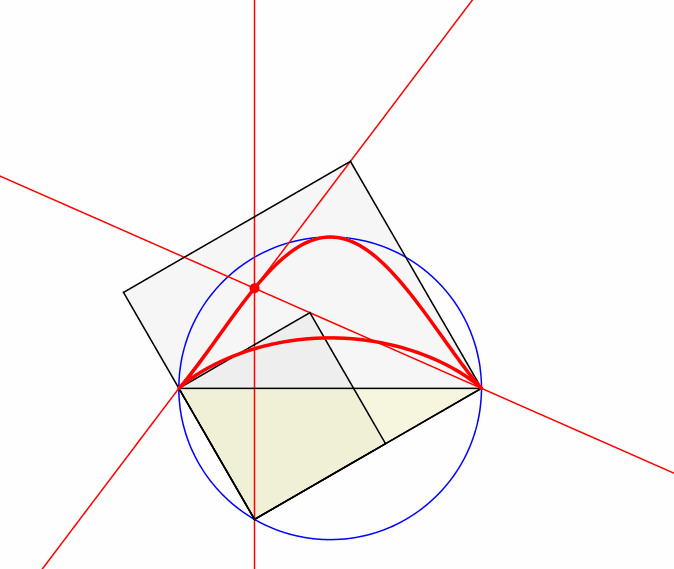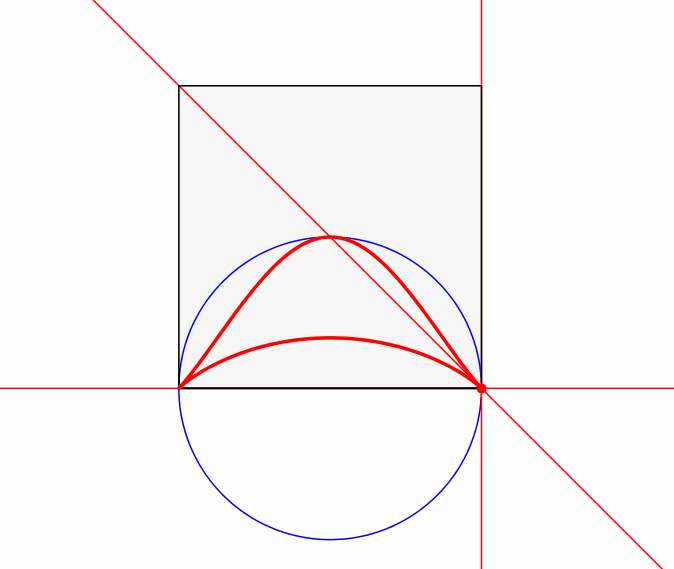
Abb. 3: Klassische Darstellung

Wir lassen die Hypotenuse fest und variieren die Ecke mit dem rechten Winkel auf dem Thaleskreis (Abb. 3). Wird die Hypotenuse als Erde gesehen und die Ecke mit dem rechten Winkel als Sonne, haben wir ein geozentrisches Weltbild.

3.2 Heliozentrisch

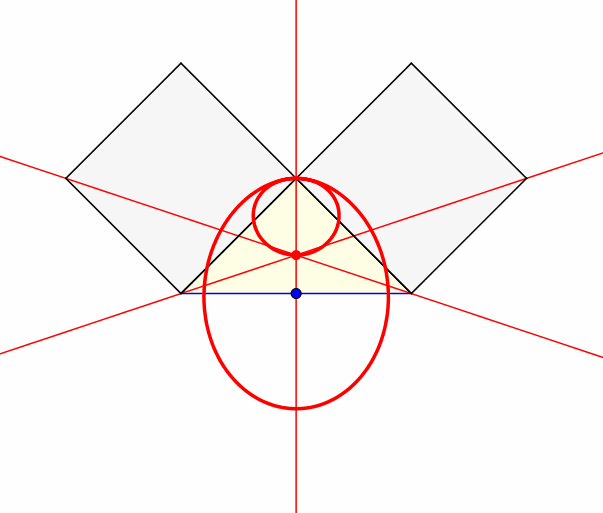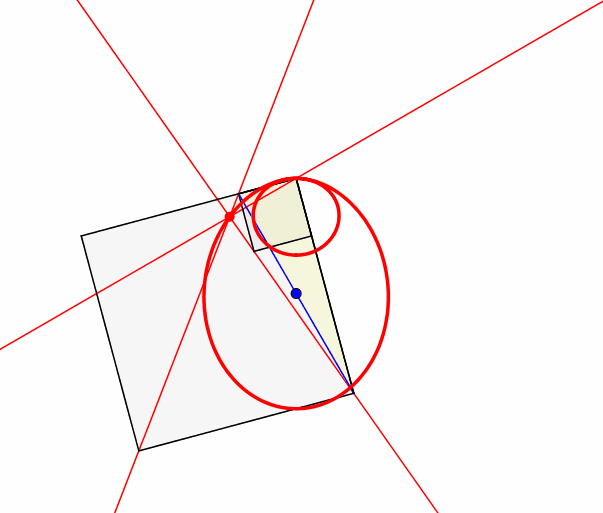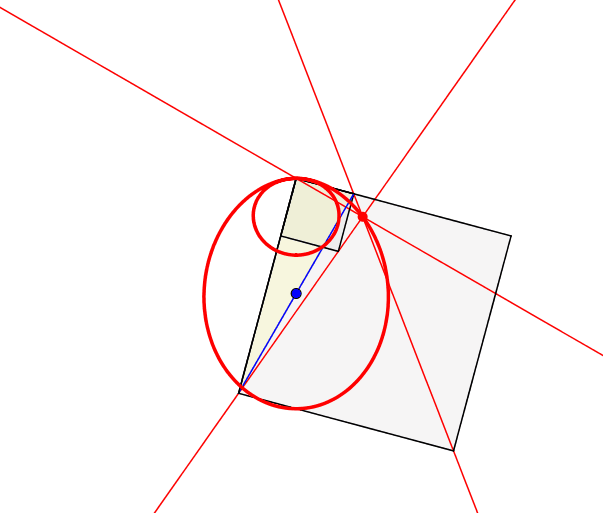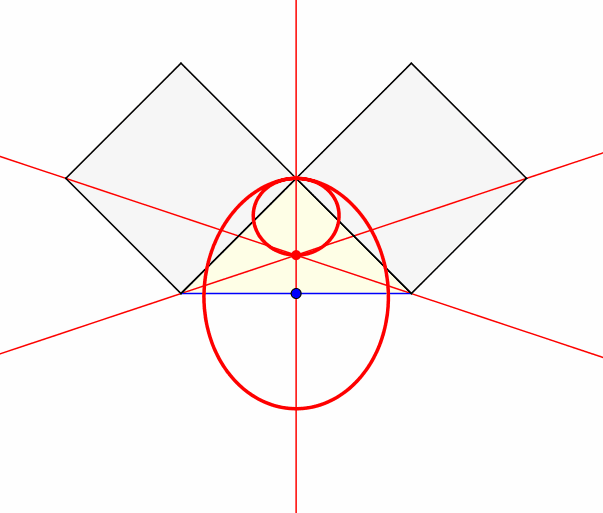
Abb. 4: Heliozentrisch

Im Sinne einer kopernikanischen Wende lassen wir die Ecke mit dem rechten Winkel fest und drehen die Hypotenuse um ihren Mittelpunkt.

3.3 Leiter an der Wand

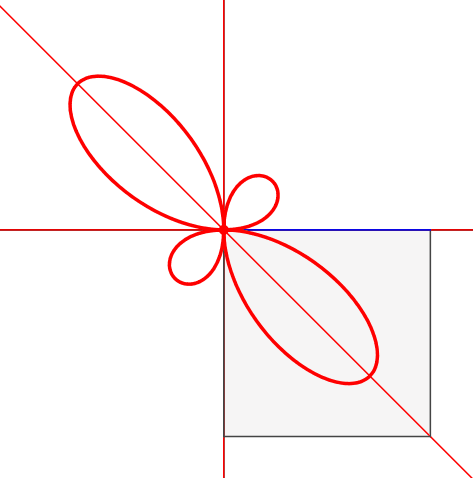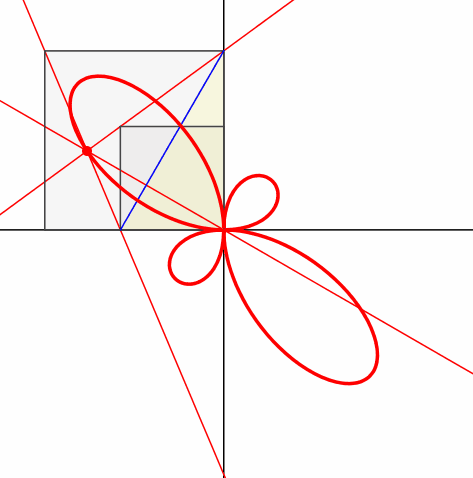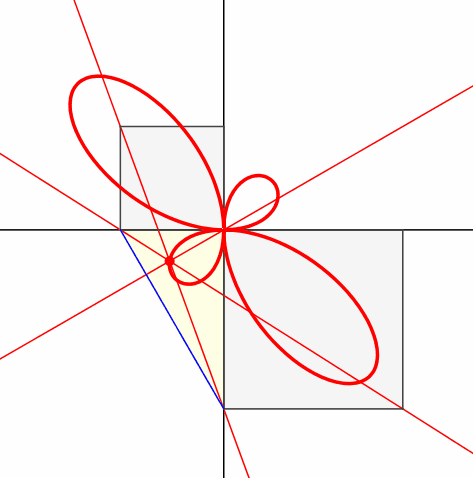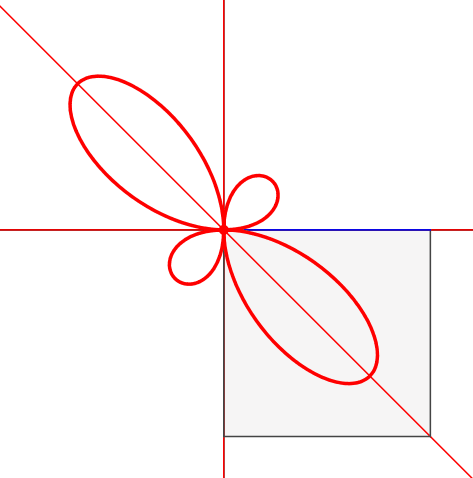
Abb.5: Leiter an der Wand

Die Position des rechtwinkligen Dreieckes (Abb. 5) entspricht den Leiter-an-der-Wand-Aufgaben. Bei der Leiterlänge 2 hat die Bahnkurve des Euklid-Punktes die Parameterdarstellung:

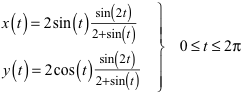(3)

3.4 Komplementär

Wir ergänzen das Leiter-an-der-Wand-Dreieck zu einem Rechteck und arbeiten mit dem Ergänzungsdreieck (Abb. 6).

Abb. 6: Ergänzungsdreieck

4 Ausblick

Der Euklid-Punkt im rechtwinkligen Dreieck ist ein Sonderfall des entsprechenden Punktes in einem allgemeinen Dreieck (Abb. 7).

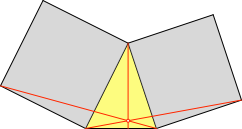
Abb. 7: Allgemein

Literatur

Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X

Gerwig, Mario (2021): Der Satz des Pythagoras in 365 Beweisen. Mathematische, kulturgeschichtliche und didaktische Überlegungen zum vielleicht berühmtesten Theorem der Mathematik. Mit einem Geleitwort von Günter M. Ziegler. Springer Spektrum. ISBN 978-3-662-62885-0. ISBN 978-3-662-62886-7 (eBook). https://doi.org/10.1007/978-3-662-62886-7