Hans Walser, [20210807]

Euklid-Punkt

Anregung: Gerwig 2021

1 Worum geht es?

Ein Schnittpunkt im rechtwinkligen Dreieck und im Kontext eines Quadrates. Anwendung des Satzes von Ceva.

2 Der Euklid-Punkt

Euklid (Euklid 1980, S. 32, Gerwig 2021, S. 20, 136, 319) illustriert den Beweis desjenigen Satzes, der heute als Satz von Pythagoras bezeichnet wird (Euklid verwendet diese Bezeichnung nicht), die Figur der Abbildung 1a (Nachzeichnung durch den Autor).

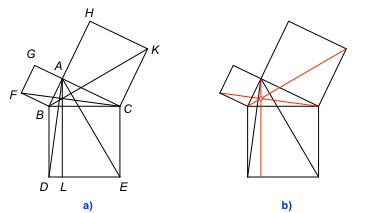
Abb. 1: Der Euklid-Punkt

Vermutung: Die drei rot markierten Geraden (Abb. 1b) haben einen gemeinsamen Schnittpunkt, den Euklid-Punkt.

3 Beweis

Für den Beweis arbeiten wir mit dem Satz von Ceva.

Das Hypotenusenquadrat ist für die Formulierung des Schnittpunktes irrelevant und wird daher im Folgenden weggelassen.

Wir arbeiten mit den Bezeichnungen der Abbildung 2.

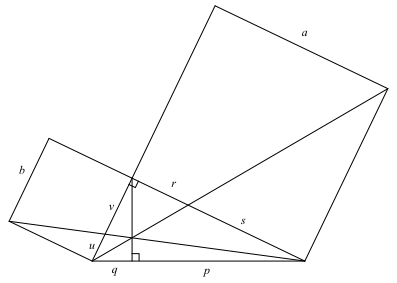
Abb. 2: Bezeichnungen

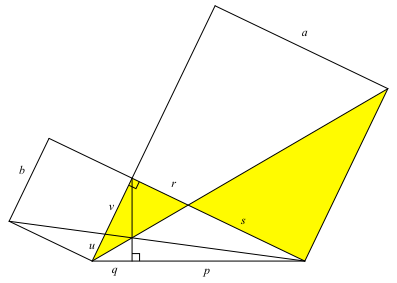
Abb. 3: Ähnliche Dreiecke

Aus der Ähnlichkeit der beiden in der Abbildung 3 gelb markierten Dreiecke folgt:

(1)

Analog:

(2)

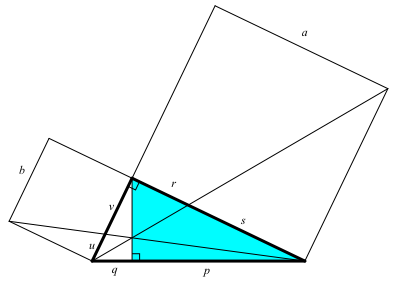
Abb. 4: Noch mehr ähnliche Dreiecke

Aus der Ähnlichkeit der beiden in der Abbildung 4 markierten Dreiecke folgt der sogenannte Kathetensatz:

(3)

Analog:

(4)

Aus (3) und (4) ergibt sich:

(5)

Aus (1), (2) und (5) erhalten wir:

(6)

Nach dem Satz von Ceva ist damit die Schnittpunkteigenschaft bewiesen. Den Schnittpunkt nennen wir Euklid-Punkt.

4 Gleiche Abschnitte

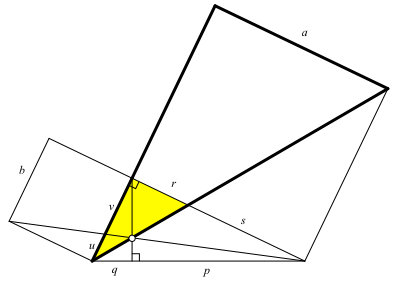
Abb. 5: Schon wieder ähnliche Dreiecke

Aus der Ähnlichkeit der beiden in der Abbildung 5 markierten Dreiecke folgt:

(7)

Analog:

(8)

Somit ist:

(9)

5 Einbeschriebenes Quadrat

Wir beschreiben dem rechtwinkligen Dreieck ein Quadrat ein (Abb. 6).

Abb. 6: Einbeschriebenes Quadrat

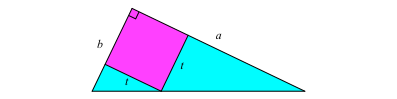
Abb. 7: Und wieder ähnliche Dreiecke

Für die Quadratseite t folgt aus der Ähnlichkeit der markierten Dreiecke in der Abbildung 7:

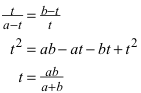(10)

Wegen (9) ist (Abb. 8):

(11)

Abb. 8: Einbeschriebenes Quadrat und Euklid-Punkt

Die Abbildung 9 zeigt den Funktionsgrafen von t in die Abhängigkeit von a und b. Nicht sehr spannend.

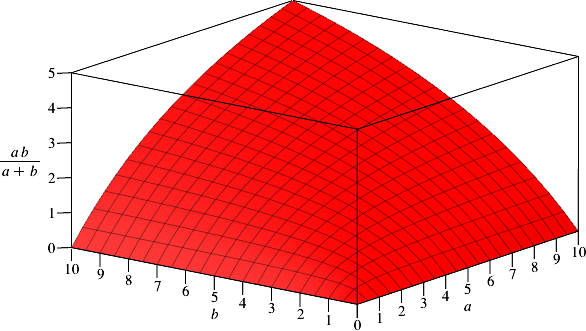
Abb. 9: Funktionsgraf

6 Euklid-Punkt mit dem eingeschriebenen Quadrat

Wir können die Kathetenquadrate weglassen und den Euklid-Punkt mit dem einbeschriebenen Quadrat formulieren (Abb. 10).

Abb. 10: Euklid-Punkt mit einbeschriebenem Quadrat

7 Bahnkurven

7.1 Festes Quadrat

Die Katheten des rechtwinkligen Dreiecks seien die Koordinatenachsen, das Quadrat das Einheitsquadrat. Die Hypotenuse geht durch die freie Ecke des Quadrates (Abb. 11).

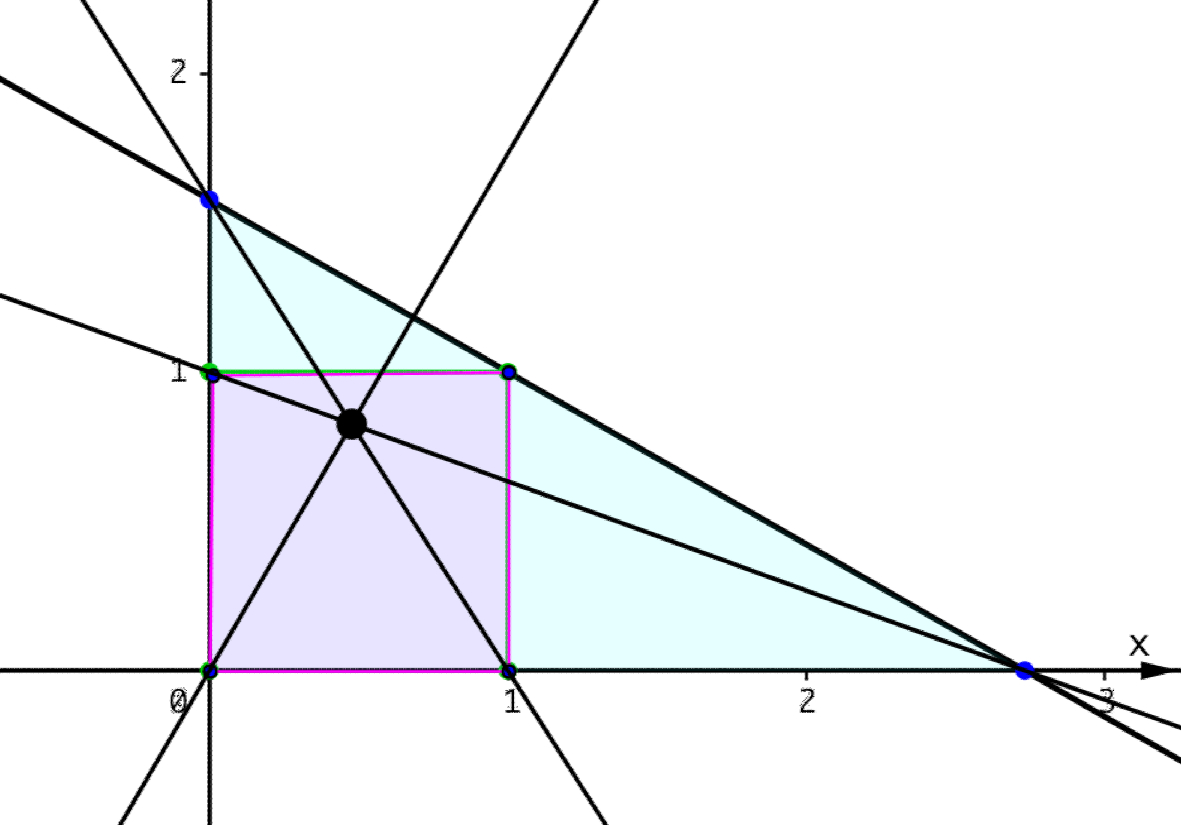
Abb. 11: Quadrat fest

Nun drehen wir die Hypotenuse (Abb. 12).

Abb. 12: Bahnkurve des Euklid-Punktes

Die Bahnkurve des Euklid-Punktes ist die Ellipse mit der Gleichung:

(12)

Nachweis rechnerisch.

7.2 Feste Hypotenuse

Wir lassen die Hypotenuse fest und drehen das Quadrat um die freie Ecke (Abb. 13).

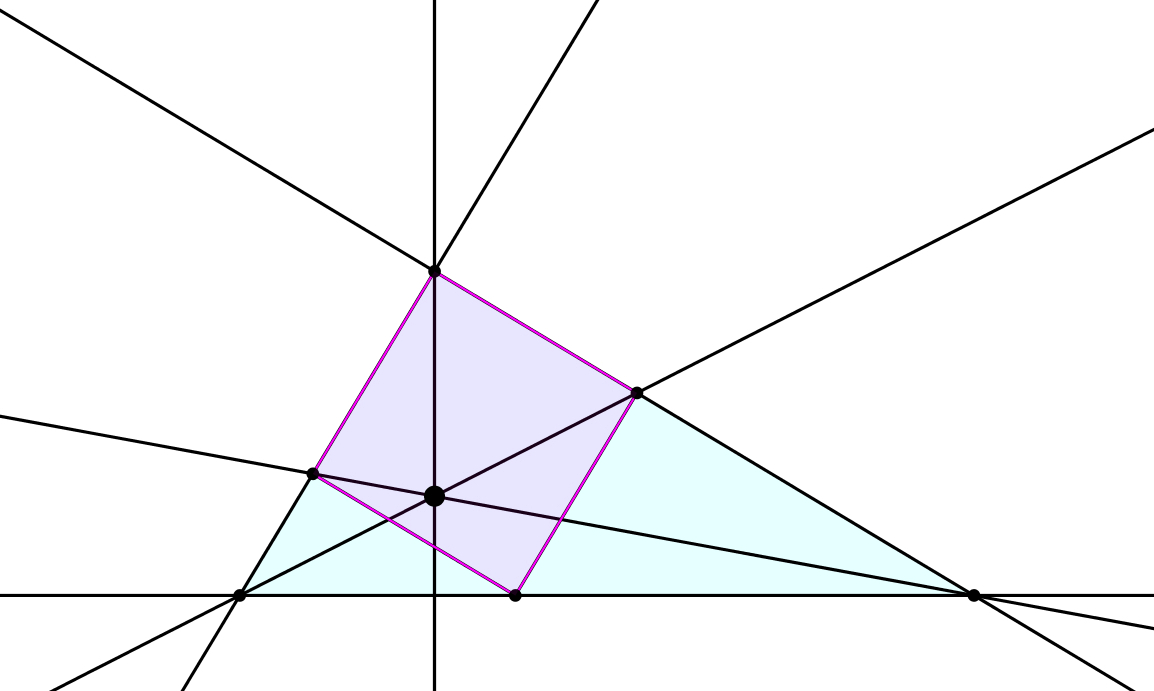
Abb. 13: Hypotenuse fest

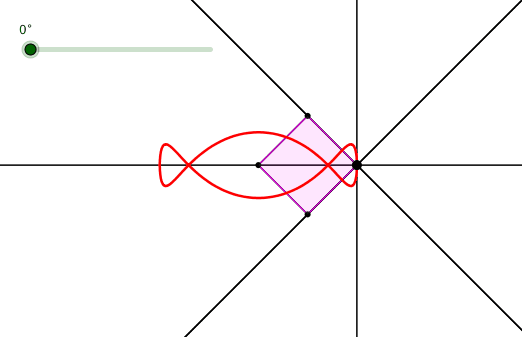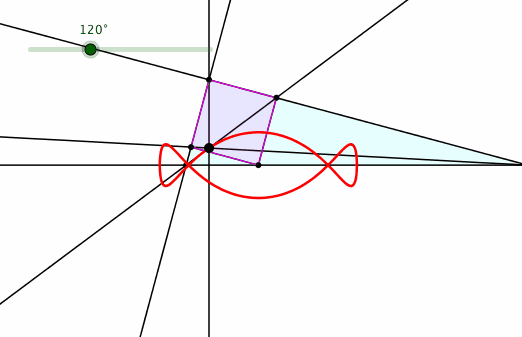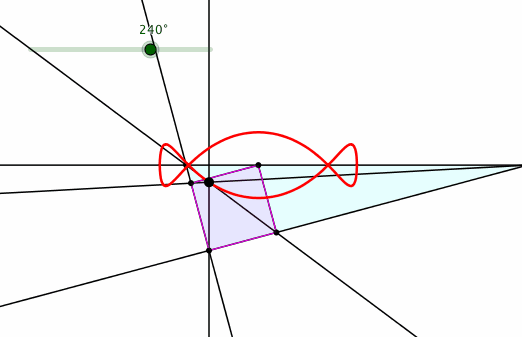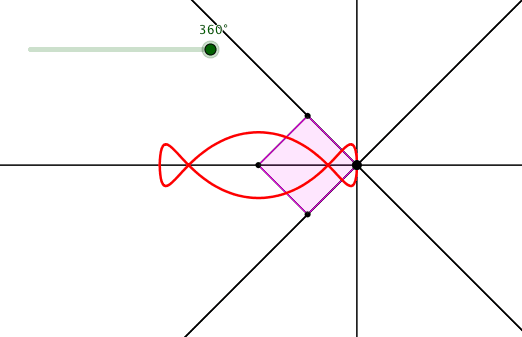
Abb. 14: Bahnkurve des Euklid-Punktes

Die Bahnkurve sieht interessant aus.

8 Ausblick

Der Euklid-Punkt im rechtwinkligen Dreieck ist ein Sonderfall des entsprechenden Punktes in einem allgemeinen Dreieck (Abb. 15).

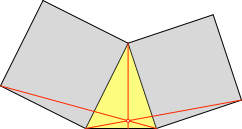
Abb. 15: Allgemein

Literatur

Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X

Gerwig, Mario (2021): Der Satz des Pythagoras in 365 Beweisen. Mathematische, kulturgeschichtliche und didaktische Überlegungen zum vielleicht berühmtesten Theorem der Mathematik. Mit einem Geleitwort von Günter M. Ziegler. Springer Spektrum. ISBN 978-3-662-62885-0. ISBN 978-3-662-62886-7 (eBook). https://doi.org/10.1007/978-3-662-62886-7

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Websites

Hans Walser: Euklid-Punkt und seine Bahnkurven

http://www.walser-h-m.ch/hans/Miniaturen/E/Euklid-Punkt/Euklid-Punkt.html

Hans Walser: Miniaturen: Pythagoras, Flächensummen und rechtwinkliges Dreieck

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Pythagoras/index.html

Hans Walser: Schnittpunkte

http://www.walser-h-m.ch/hans/Schnittpunkte/index.html