Hans Walser, [20171015]
Eulersche Polyederformel
1 Worum geht es?
Die Eulersche Polyederformel wird in der Schule meist durch Abzhlen der Ecken, Kanten und Flchen bearbeitet.
Es wird fr einigerma§en regelm§ige Polyeder eine alternative Berechnungsart vorgestellt, welche sich auch auf ebene und hyperbolische ãPolyederÒ bertragen lsst.
Vorgehen exemplarisch.
2 Beispiele mit Polyedern
2.1 Wrfel
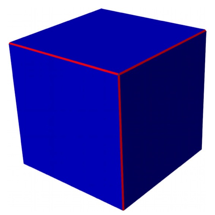
Abb. 1: Wrfel
2.1.1 Globales Vorgehen
Der Wrfel hat e = 8 Ecken, k = 12 Kanten und f = 6 Flchen. Daraus ergibt sich:
![]() (1)
(1)
Wir knnen alternativ vorgehen wie folgt.
2.1.2 Lokales Vorgehen
Von jeder Wrfelecke gehen drei Kanten aus. Da jede Kante zwei Wrfelecken verbindet, erhalten wir fr die Anzahl k der Kanten:
![]() (2)
(2)
Weiter kommen an jeder Wrfelecke drei Quadratflchen zusammen. Da jede Quadratflche mit vier Ecken inzidiert, erhalten wir fr die Anzahl f der Flchen:
![]() (3)
(3)
Somit ist:
![]() (4)
(4)
Wegen e = 8 folgt (1). Wir mssen nur einmal global zhlen.
2.1.3 Winkeldefizit
An jeder Ecke kommen drei rechte Winkel von den Quadratflchen zusammen. Das macht zusammen 270¡. Es fehlen 90¡ bis zum vollen Winkel von 360¡. Auf e = 8 Ecken fehlen also insgesamt 8 × 90¡ = 720¡. Das ist das globale Winkeldefizit nach Descartes. Damit wird:
![]() (5)
(5)
Die Herleitung ber das Winkeldefizit ist ebenfalls lokal. Wir brauchen nur noch die Eckenzahl zu kennen.
2.2 Kuboktaeder

Abb. 2: Kuboktaeder
2.2.1 Globale Zhlweise
Das Kuboktaeder hat e = 12 Ecken, k = 24 Kanten und f = 14 Flchen. Somit ist:
![]() (6)
(6)
2.2.2 Lokale Zhlweise
Von jeder Ecke gehen vier Kanten aus. Somit ist:
![]() (7)
(7)
An jeder Ecke kommen zwei Quadrate und zwei Dreiecke an. Daher ist:
![]()
Daher erhalten wir:
![]() (8)
(8)
Wegen e = 12 folgt ![]() .
.
2.2.3 Winkeldefizit
An jeder
Ecke haben wir zwei 60¡-Winkel und zwei 90¡-Winkel, zusammen also 300¡. Das
Winkeldefizit ist 60¡. Wegen e = 12
ist das globlae Winkeldefizit 720¡ und damit ![]() .
.
2.3 Rhombitruncated Icosidodcahedron
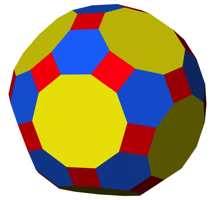
Abb. 3: Rhombitruncated Icosidodecahedron
2.3.1 Globale Zhlweise
Es ist e = 120, k = 180 und f = 12 + 20
+ 30 = 62. Wer zhlt nach? Es ist ![]() .
.
2.3.2 Lokale Zhlweise
Von jeder Ecke gehen drei Kanten aus. Daher ist:
![]() (9)
(9)
Jede Ecke inzidiert mit einem Zehneck, einem Sechseck und einem Quadrat. Daher ist:
![]() (10)
(10)
Somit:
![]() (11)
(11)
Wegen e = 120 ist ![]() .
.
2.3.3 Winkeldefizit
An jeder
Ecke haben wir einen Winkel von 144¡ (Zehneck), einen Winkel von 120¡
(Sechseck) und einen Winkel von 90¡ (Quadrat), zusammen also 354¡ und ein Winkeldefizit
von 6¡. Wegen e = 120 ist das globale
Winkeldefizit 720¡ und damit ![]() .
.
3 Ebene Raster
In ebenen Rastern ist das Winkeldefizit trivialerweise null.
Zunchst die drei klassischen Raster: Karoraster, Hexagonalraster und Dreiecksraster.
3.1 Karoraster

Abb. 4: Karoraster
Im Karoraster haben wir unendlich viele Ecken, Kanten und Flchen. Wir knnen nicht global rechnen.
3.1.1 Lokale berlegung
Wir haben e Ecken.
Von jeder Ecke gehen vier Kanten aus. Daher ist:
![]() (12)
(12)
In jeder Ecke inzidieren vier Quadrate. Daher ist:
![]() (13)
(13)
Wir erhalten:
![]() (14)
(14)
Die Eckenzahl spielt in der berlegung keine Rolle.
3.1.2 Winkeldefizit
An jeder Ecke haben wir vier rechte Winkel, zusammen also 360¡. Das lokale Winkeldefizit ist null. Daher ist auch das globale Winkeldefizit null, und wir haben:
![]()
3.2 Hexagonalraster

Abb. 5: Hexagonalraster
Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (15)
(15)
3.3 Dreiecksraster

Abb. 6: Dreiecksraster
Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (16)
(16)
3.4 Sechsecke und Dreiecke

Abb. 7: Sechsecke und Dreiecke
Es ist ![]() und
und ![]() , und daher
, und daher ![]() .
.
3.5 Zwlfecke, Sechsecke und Quadrate
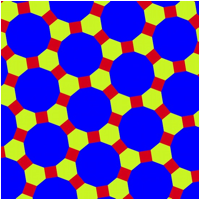
Abb. 8: Zwlfecke, Sechsecke und Quadrate
Es ist ![]() und
und ![]() , und daher
, und daher ![]() .
.
4 Hyperbolische Raster
Bei
hyperbolischen Rastern wird ![]() .
.
Das Winkeldefizit an einer Ecke wird negativ (die Winkelsumme ist gr§er als 360¡).
4.1 Siebenecke

Abb. 9: Siebenecke
Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (17)
(17)
Die Winkelsumme an einer Ecke ist:
![]() (18)
(18)
Das
Winkeldefizit an einer Ecke ist somit ![]() .
.
4.2 Allgemein
Wir
arbeiten mit n-Ecken mit n ³ 7. Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (19)
(19)
4.3 Siebenecke und Dreiecke

Abb. 10: Siebenecke und Dreiecke
Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (20)
(20)
An einer Ecke haben wir die Winkelsumme:
![]() (21)
(21)
Das
Winkeldefizit an einer Ecke ist ![]() .
.
4.4 Allgemein
Wir arbeiten mit n-Ecken (n ³ 7) und Dreiecken.
Es ist ![]() und
und ![]() . Daher ist:
. Daher ist:
![]() (22)
(22)