Hans Walser, [20140417a]

Eulergerade

1 Worum geht es

Es wird eine Methode vorgestellt, wie die Eulergerade durch den Umkreismittelpunkt allein oder auch durch den Höhenschnittpunkt allein gezeichnet werden kann.

2 Die Eulergerade

In einem Dreieck mit dem Umkreismittelpunkt U, dem Höhenschnittpunkt H und dem Schwerpunkt S liegen die drei Punkte auf einer Geraden, der Eulergeraden (Abb. 1, Walser, 2011, S. 11,12).

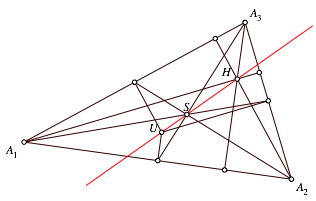
Abb. 1: Eulergerade

Die Abbildung 2 zeigt einen Beweis ohne Worte (Walser, 2007).

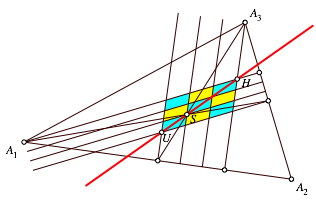
Abb. 2: Beweis ohne Worte

Für die Konstruktion der Eulergeraden genügt die Konstruktion von zweien der drei Punkte U, H, S.

3 Konstruktion mit dem Umkreismittelpunkt allein

3.1 Der Richtungsvektor

Wir konstruieren den Umkreismittelpunkt U. Damit ergeben sich die Abstandsvektoren zu den Seiten (Abb. 3). Die Summe dieser drei Abstandsvektoren ist ein Richtungsvektor der Eulergeraden.

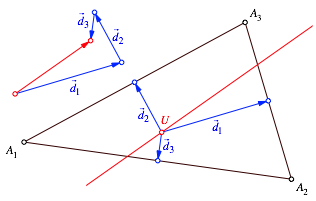
Abb. 3: Richtungsvektor der Eulergeraden

3.2 Beweis

Wir zeichnen den Feuerbach-Quader ein (Abb. 4).

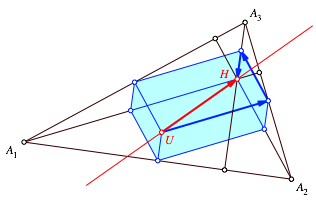
Abb. 4: Feuerbach-Quader

Unsere Vektorsumme ist zunächst ein Kantenzug auf dem Quader. Der resultierende Vektor ist der Diagonalen-Vektor . Wir haben also durch das Hintertürchen doch den Höhenschnittpunkt gezeichnet, allerdings nicht als Schnittpunkt der drei Höhen.

3.3 Variante

Wir arbeiten mit den drei Vektoren (Abb. 5). Ihre Summe ist ebenfalls der Vektor .

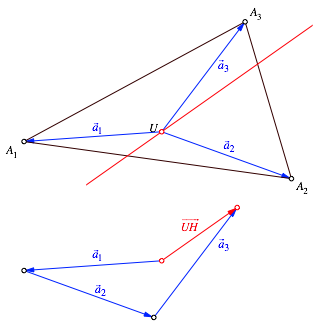
Abb. 5: Variante

Beweis: Es ist (Indizes zyklisch modulo 3). Somit ist:

3.4 Kombinatorisches

Es gibt 3! = 6 Möglichkeiten, die Summe von drei Vektoren darzustellen (Abb. 5).

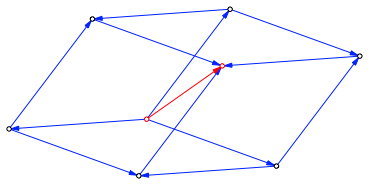
Abb. 6: Würfel?

Es entsteht eine gleichseitige Figur aus sechs Rhomben. Wir sind geneigt, diese Figur räumlich zu sehen, sollten sie aber flach sehen.

Wir können nun auf 8 Arten drei Punkte auswählen, welche auf das blaue Kantengerüst bezogen je die Hamming-Distanz 2 haben. Hamming-Distanz 2 heißt: Ein Kantenkäfer der sich nur entlang der blauen Kanten bewegen kann, muss genau zwei Kanten von einem Punkt zum anderen zurücklegen.

Das kann man sich so überlegen: Wir wählen einen von den acht Punkten und nehmen die drei anderen Endpunkte der von diesem Punkt ausgehenden Kanten. In der Abbildung 7 sind die drei zum roten Punkt links benachbarten Punkte ausgewählt und zum Dreieck verbunden.

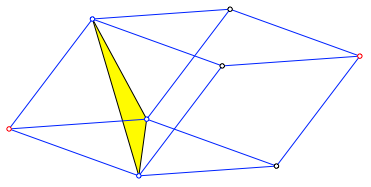
Abb. 7: Dreieck in der Rhombenfigur

Der rote Punkt ganz links ist dann der Umkreismittelpunkt des Dreiecks (trivial), der dazu diametrale Punkt der Höhenschnittpunkt (weniger trivial). Die Abbildung 8 zeigt die Situation in extenso.

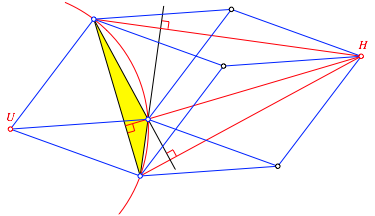
Abb. 8: Umkreismittelpunkt und Höhenschnittpunkt

Wir versuchen nun, die Figur doch räumlich zu sehen (Abb. 9) und schneiden das gelbe Dreieck mit der Raumdiagonalen UH.

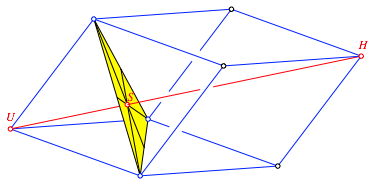
Abb. 9: Räumliche Sicht

Der Schnittpunkt ist der Schwerpunkt S des gelben Dreiecks. Planimetrisch gesehen ist die Gerade UH die Eulergerade des gelben Dreiecks. Damit sind wir wieder beim Thema.

4 Konstruktion mit dem Höhenschnittpunkt allein

Wir zeichnen den Höhenschnittpunkt H und dazu die Abstandsvektoren zu den Ecken (Abb. 10). Die Summe dieser Abstandsvektoren ist ebenfalls ein Richtungsvektor der Eulergeraden.

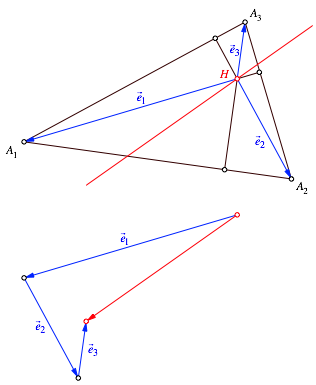
Abb. 10: Richtungsvektor der Eulergeraden

Wegen ist dies aber nur eine Variante der Konstruktion mit dem Umkreismittelpunkt.

Literatur

Walser, Hans (2007): Die Eulersche Gerade. Beweis ohne Worte. UNI NOVA Wissenschaftsmagazin der Universität Basel. 105 – März 2007. 20.

Walser, Hans (2011): Geometrische Miniaturen. Figuren – Muster – Symmetrien. Leipzig. EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-42-4.