1 Worum geht es?

Ein Zugang zur Eulergeraden mit Schnittpunkten.

2 Ausgangslage

Den drei Seiten eines beliebigen Dreieckes setzen wir drei zueinander ähnliche gleichschenklige Dreiecke an gemäß Abbildung 1. Die Basen der gleichschenkligen Dreiecke sitzen auf den Dreiecksseiten.

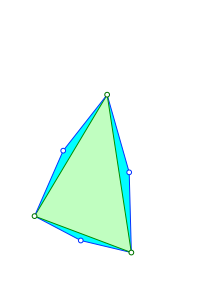
Abb. 1: Gleichschenklige Dreiecke ansetzen

Nun verlängern wir die Schenkel der gleichschenkligen Dreiecke bis sie sich wechselseitig schneiden gemäß Abbildung 2. Gegebenenfalls müssen die Schenkel auch nach hinten verlängert werden, geometrisch also als unendlich lange Geraden interpretiert werden.

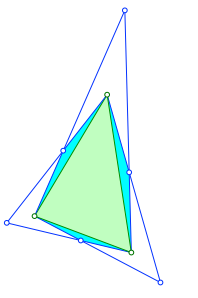
Abb. 2: Verlängern bis zum Schnitt

Diese neuen Schnittpunkte und die gegenüberliegenden alten Schnittpunkte verbinden wir je mit einer Geraden (rot in Abbildung 3). Die drei Geraden schneiden sich in einem Punkt. Verifikation mit DGS.

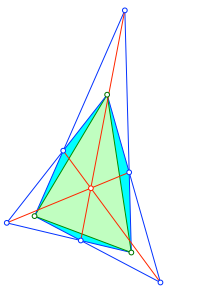
Abb. 3: Schnittpunkt

3 Kinematik

Nun variieren wir den gemeinsamen Basiswinkel der angesetzten gleichschenkligen Dreiecke (Abb. 4). Die gleichschenkligen Dreiecke selber sind nicht mehr gezeichnet, um die Figur nicht zu überladen.

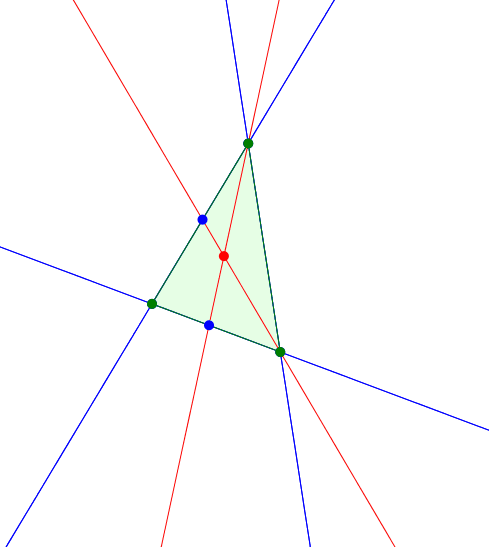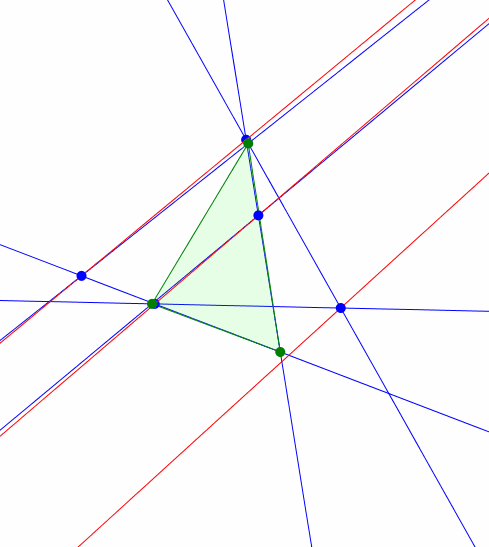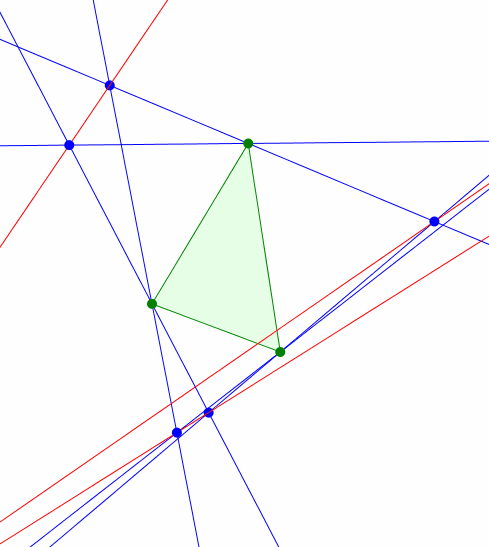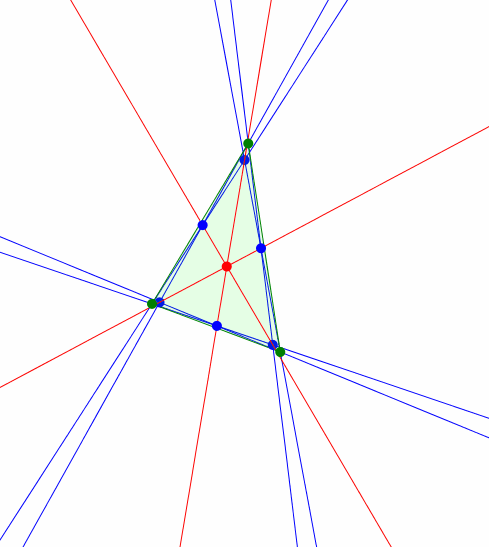
Abb. 4: Variation der Basiswinkel

Wir vermuten, dass der rote Schnittpunkt sich auf einer Geraden bewegt. Dies ist auch richtig (Verifikation mit DGS). Es handelt sich um die Eulergerade (Abb. 5).

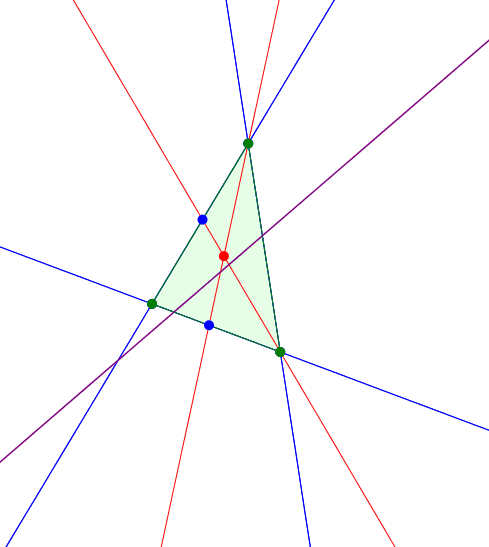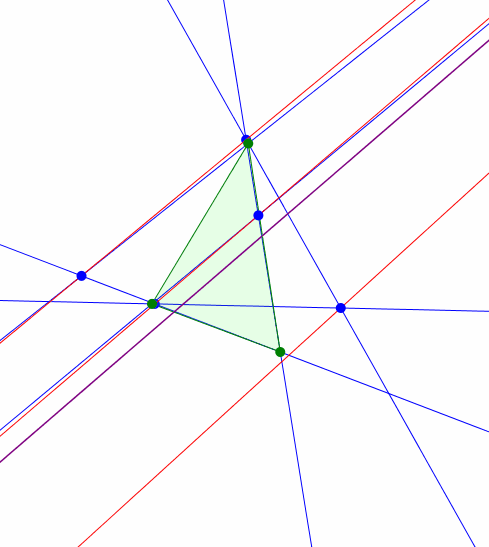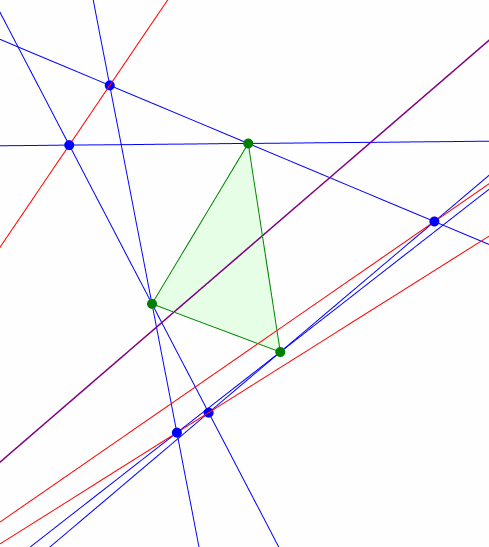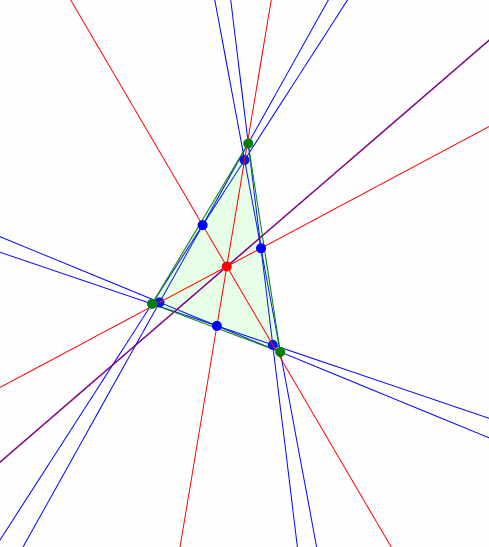
Abb. 5: Eulergerade

Allerdings sehen wir, dass der rote Schnittpunkt ein Stück der Eulergeraden ausblendet. Es handelt sich um das Stück vom Schwerpunkt des Ausgangsdreieckes bis zum Punkt, der sich als Spiegelbild des Höhenschnittpunktes bei Spiegelung am Umkreismittelpunkt ergibt.

In der Abbildung 6 ist das ausgeblendete Stück dünn gezeichnet, der Rest dick.

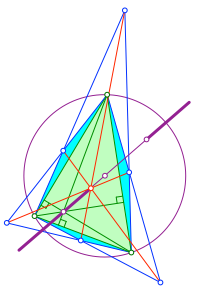
Abb. 6: Ausgeblendetes Stück auf der Eulergeraden

Weblinks

Hans Walser: Euler-Gerade

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade/Eulergerade.htm

Hans Walser: Eulergerade

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade2/Eulergerade2.htm

Hans Walser: Ein merkwürdiger Punkt auf der Eulergeraden

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade3/Eulergerade3.htm

Hans Walser: Kiepert-Gerade

http://www.walser-h-m.ch/hans/Miniaturen/K/Kiepert-Gerade/Kiepert-Gerade.html