Hans Walser, [20190331]

Evolvente

Anregung: Hans-Peter Stricker, Berlin

1     Worum geht es?

Auf der Kreisevolvente (auch Kreisinvolute) werden Punkte in gleichen BogenabstŠnden gezeichnet. Je nach Abstand entstehen schšne oder regelmŠ§ige Muster.

Ebenso werden Wellenlinien (Sinuskurven) gezeichnet.

Ein Bilderbuch.

2     Kreisevolvente

Die Abbildung 1 zeigt die Evolvente fŸr den Kreis mit dem Radius . Dieser Kreis (blau in Abb. 1) hat den Umfang 1.

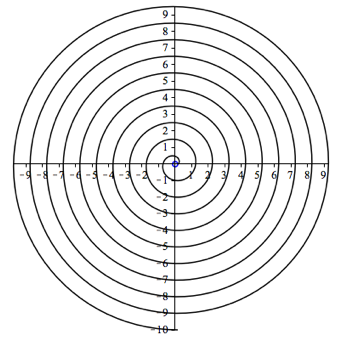
Abb. 1: Kreisevolvente

Diese Kreisevolvente hat die Parameterdarstellung:

 

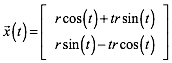                                                                                 (1)

 

 

 

 

Sie hat das recht einfache Bogenelement:

 

                                                                                                                         (2)

 

 

 

FŸr die Berechnung der BogenlŠnge von 0 bis zum Parameterwert t gilt daher:

 

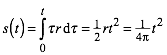                                                                                  (3)

 

 

 

 

3     €quidistante Punkte

Wir zeichnen nun Punkte im Bogenabstand (das hei§t auf der Evolvente gemessen) a. Der Parameter  fŸr den n-ten Punkt erhalten wir aus (3):

 

                                                                   (4)

 

 

 

FŸr verschiedene Werte von a ergeben sich ãschšneÒ oder regelmŠ§ige Muster.

Abb. 2.1: a = 1

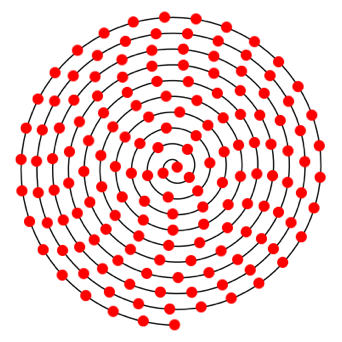
Abb. 2.2: a = 2

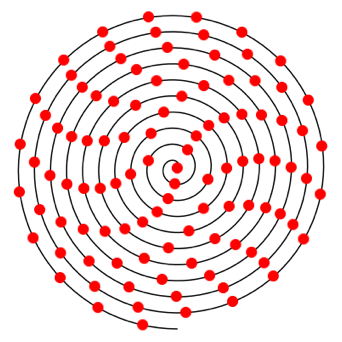
Abb. 2.3: a = 3

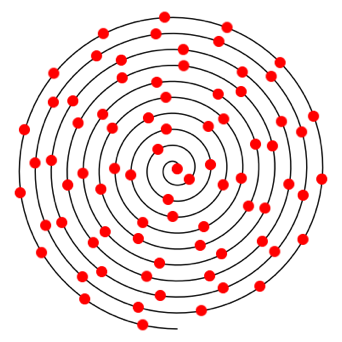
Abb. 2.4: a = 4

Abb. 2.5: a = ¹/2

Abb. 2.6: a = ¹/3

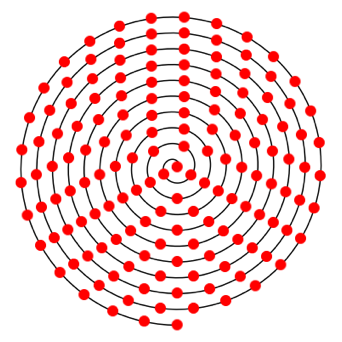
Abb. 2.7: a = 2*¹/3

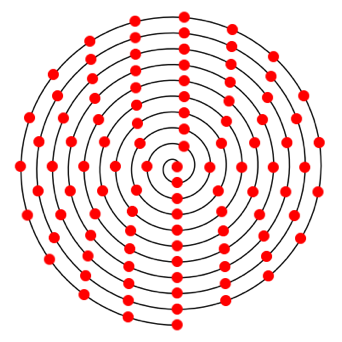
Abb. 2.8: a = ¹

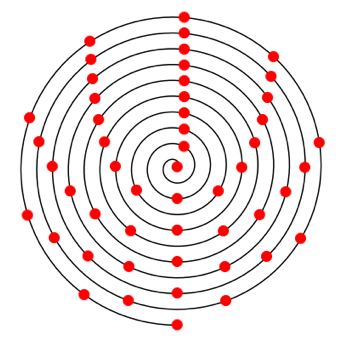
Abb. 2.9: a = 2¹

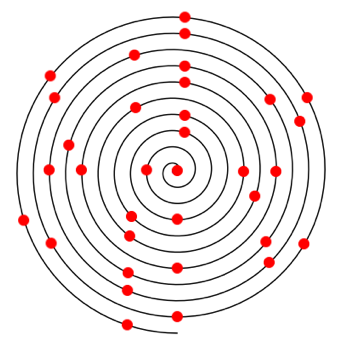
Abb. 2.10: a = 3¹

4      

5     Wellenlinien

In der Abbildung 3 ist der Evolvente eine Sinuslinie mit der Frequenz f = 1 aufmoduliert. Die Wellenlinie w hat mit der Frequenz f die Parameterdarstellung:

 

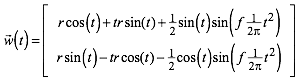                                      (5)

 

 

 

 

 

FŸr verschiedene Werte von f ergeben sich ãschšneÒ oder regelmŠ§ige Muster.

 

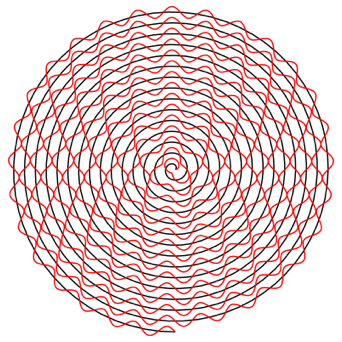
Abb. 3: Wellenlinie. Frequenz 1

In den folgenden Abbildungen wird die Frequenz variiert.  Die Evolvente ist jeweils nicht mehr gezeichnet.

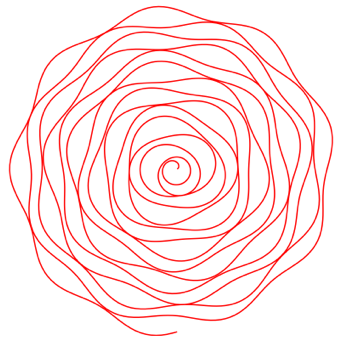
Abb. 4.1: Frequenz 0.03

Abb. 4.2: Frequenz 1/2

Abb. 4.3: Frequenz 0.95

Abb. 4.4: Frequenz 0.97

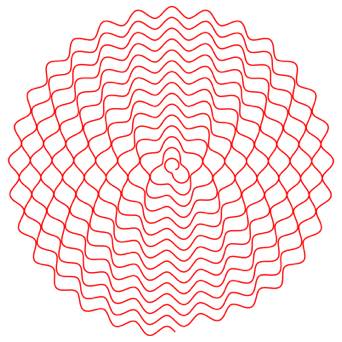
Abb. 4.5: Frequenz 1

Abb. 4.6: Frequenz 1.45

Abb. 4.7: Frequenz 1.53

Abb. 4.8: Frequenz ¹/2

Abb. 4.9: Frequenz 1.95

Abb. 4.10: Frequenz 2

Abb. 4.11: Frequenz 2.03

Abb. 4.12: Frequenz 5/2

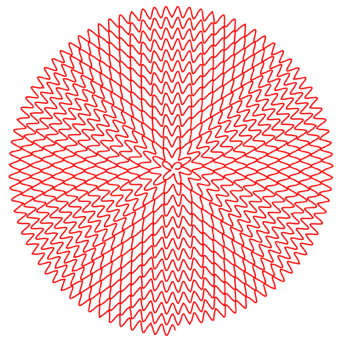
Abb. 4.13: Frequenz 3

6     Parallel-Eigenschaft der Kreisevolvente

Die in der Abbildung 5 blau angegebenen Geraden sind parallel. Der Parameter t ist also auch der Steigungswinkel der zugehšrigen Tangenten (modulo 2¹). Der Abstand zwischen zwei aufeinanderfolgenden Tangenten ist konstant 2r¹. Die Evolvente ist also Ÿberall gleich ãdickÒ.

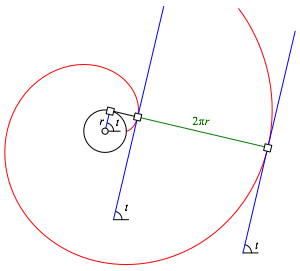
Abb. 5: Parallelen

Damit wird es sehr einfach, die Evolvente mit Rechtecken zu versehen, die sich an der jeweiligen Evolventen-Richtung orientieren. FŸr die Rechtecke verwenden wir die LŠnge a und die Breite 1.

7     Quadrate und Rechtecke

Die Abbildung 6 zeigt die Situation fŸr Quadrate, also a = 1. Die Quadrate sind von Innen nach au§en nummeriert.

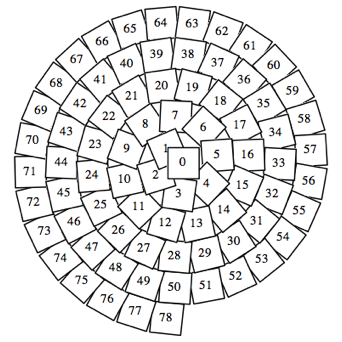
Abb. 6: Quadrate

Die Abbildung 7 zeigt die Situation fŸr a = 3.

Abb. 7: a = 3

Die Abbildung 8 zeigt dasselbe mit den alternierenden Farben rot und blau.

Abb. 8: Alternierende Farben

In der Abbildung 9 wurde a = ¹ gewŠhlt.

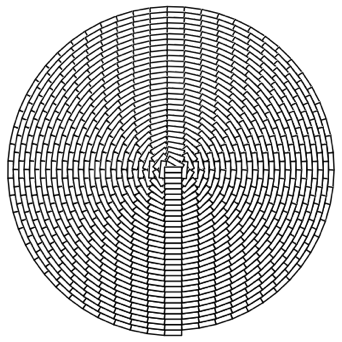
Abb. 9: a = ¹

Die Abbildung 10 zeigt dasselbe in alternierenden Farben.

Abb. 10: Alternierende Farben

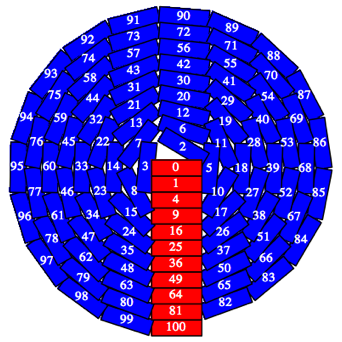
Abb. 11: Ohne Kommentar