Hans Walser, [20130122]

Exponentialfunktion und Potenzfunktion

Anregung: Ch. W., B.

1 Worum es geht

Dieser Abschnitt enthält nur didaktische Vorbemerkungen, kann also übersprungen werden.

Im konventionellen Unterricht wird die Potenzfunktion vor der Exponentialfunktion behandelt. Man kann sich überlegen, was es bringt, die Reihenfolge zu vertauschen. Schließlich ist ja die Exponentialfunktion neben der linearen Funktion die wohl wichtigste Funktion überhaupt.

In der Didaktik ist es üblich, dass einer, der etwas Neues einführen möchte, zuerst mal das Bisherige schlecht macht, auf dass sein Leuchtturm umso heller in der Finsternis leuchte. Machen wir also die Potenzfunktion schlecht:

Das Ableiten ist eine mühsame Geschichte. Bei der Quadratfunktion geht es noch, die Ableitung der kubischen Funktion wird als Hausaufgabe gegeben und für die Potenzfunktionen ahnt man, dass es vermöge der binomischen Formel wohl auch so geht. Und dann schiebt der Lehrer noch die gebrochenen und die irrationalen Exponenten nach und hofft, dass die Schüler das schlucken. Gewissenhaft Lehrer leiten wenigsten die Ableitung der Quadratwurzelfunktion mit einigem Aufwand neu her.

Beim Integrieren wiederholt sich das ganze Theater in grün. Zudem hat man den hässlichen Sonderfall der umgekehrten Proportionalität, der nicht ins Schema passt wegen der verbotenen Division durch Null und wunderbarer- aber unerklärlicherweise zum natürlich Logarithmus führt. Dieser ist aber für die Schüler zu diesem Zeitpunkt alles andere als natürlich.

Ganz schlimm wird es, wenn man sich im Unterricht auf die Potenzfunktionen beschränkt. Das führt dann zum falschen Bild, dass Mathematik etwa darin besteht, den Wendepunkt einer kubischen Parabel zu bestimmen.

2 Die Exponentialfunktion

2.1 Die Exponentialfunktion als solche

Die Exponentialfunktion ist die Lösung der Differentialgleichung mit der Bedingung .

Die Abbildung 1 zeigt das Richtungsfeld , die Anfangsbedingung als Punkt und die Lösungskurve.

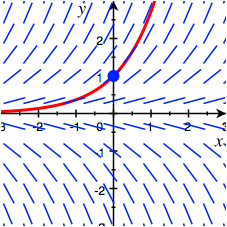
Abb. 1: Exponentialfunktion

Die Exponentialfunktion wird mit oder konventionell mit geschrieben, die zugehörige Umkehrfunktion mit .

2.2 Eine parametrisierte Kurve

Welche Kurve ergibt sich durch die Parameterdarstellung

Natürlich erwarten wir so etwas wie die Exponentialkurve. Der Plot belehrt uns besser (Abb. 2).

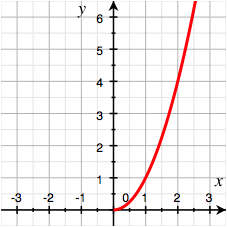
Abb. 2: Was für eine Kurve ist das?

Das sieht doch eher aus wie die rechte Hälfte der Standardparabel. Und in der Tat:

Da wir nur die rechte Hälfte haben, ergibt sich erst noch der Vorteil der Umkehrbarkeit.

Analog führt die Parameterdarstellung

zur Kurve . Für natürliche Zahlen s haben wir somit die Potenzfunktionen im Kasten, für negative s die gebrochenen Funktionen, insbesondere die indirekte Proportionalität, für gebrochene s die Wurzelfunktionen und für reelle s Funktionen, deren Name ich nicht weiß.

Dieses ganze Theater macht natürlich nur Sinn, wenn man es brauchen kann. Ästhetik ist in unserer nützlichkeitsorientierten Kultur kein Kriterium. Also:

2.3 Ableitung

Zur Kurve

berechnen wir nun mal den Tangentialvektor. Dies ist besonders einfach, weil wir die Ableitung der Exponentialfunktion von der Definition her kennen. Es ist:

Der Tangentialvektor hat die Steigung:

Wegen erhalten wir:

Somit ist . Das geht so für sämtliche s.

2.4 Integration

Wir wollen das bestimmte Integral gemäß Abbildung 3 bestimmen.

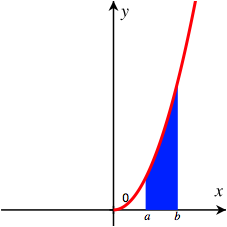
Abb. 3: Integral

Die Kurve ist durch

gegeben ist. Wir haben also die Kurve und das bestimmte Integral

zu berechnen. Dazu arbeiten wir mit der Substitution . Damit ist und weiter:

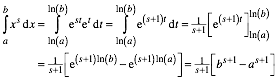
Wir sehen, dass die Funktion die Stammfunktion hat. Der Fall muss auch hier separat behandelt werden, geht aber sehr einfach:

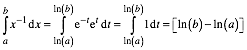
Somit hat die Funktion den natürlichen Logarithmus als Stammfunktion.

3 Zusammenfassung

Bei Kenntnis der Exponentialfunktion lassen sich Ableitung und Integration der Potenz- und Wurzelfunktionen sehr einfach herleiten.