Hans Walser, [20150439]
Exponentieller Zerfall und periodischer Nachschub
1 Problemstellung
Die Wirkstoffe eines Medikamentes werden im Kšrper im Sinne eines exponentiellen Zerfalls abgebaut.
Wie verhŠlt sich die Wirkstoffmenge im Kšrper wenn das Medikament in regelmŠ§igem Abstand eingenommen wird?
2 Beispiel
Die Wirkstoffmenge habe im Kšrper die Halbwertszeit 1. Pro Tablette werde die Wirkstoffmenge 1 eingenommen.
Bei einmaliger Tabletteneinnahme verhŠlt sich die Wirkstoffmenge im Kšrper gemŠ§ Abbildung 1. Wir haben einen klassischen exponentiellen Zerfall.
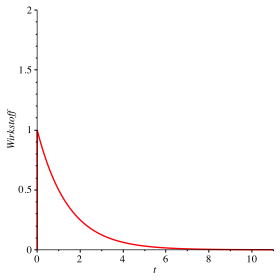
Abb. 1: Exponentielle Abnahme
Nun nehmen wir an, dass in Intervallen der Halbwertszeit je eine Tablette eingenommen wird. Die Wirkstoffmenge im Kšrper kumuliert sich gemŠ§ Abbildung 2.
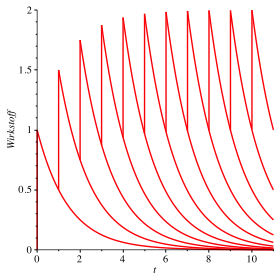
Abb. 2: Kumulierung
Die Abbildung 3 zeigt die gesamte Wirkstoffmenge im Kšrper.
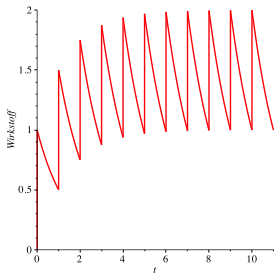
Abb. 3: Gesamte Wirkstoffmenge
Die Spitzen (Maxima unmittelbar nach der Tabletteneinnahme) nŠhern sich dem Grenzwert 2 (das ist das Doppelte der Tablettendosis), die Minima unmittelbar vor der Tabletteneinnahme nŠhern sich dem Grenzwert 1. Nach einer kurzen Startphase haben wir ein annŠhernd periodisches SŠgezahnmuster.
Die Abbildung 4 zeigt eine polygonale Approximation.
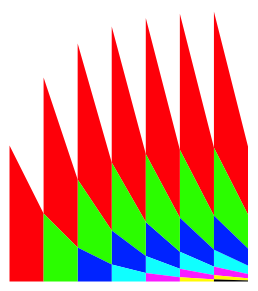
Abb. 4: Polygonale Approximation
Trapeze gleicher Farbe haben auch gleichen FlŠcheninhalt.
Von oben nach unten entwickelt sich die Reihe:
![]()
So erklŠrt sich der Grenzwert fźr die Spitzenhšhe.
3 Variation des Beispiels
Wir nehmen nun nur in AbstŠnden von zwei Halbwertszeiten eine Tablette (Abb. 5 und 6).
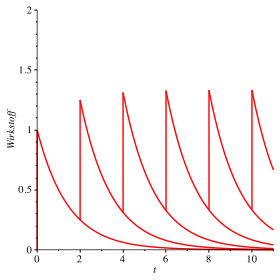
Abb. 5: Zwei Halbwertszeiten als Intervall
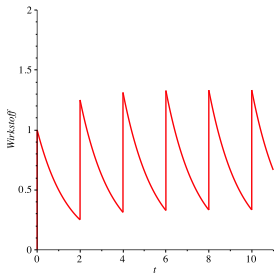
Abb. 6: Kumuliert
Fźr die
Spitzen erhalten wir den Grenzwert ![]() , fźr die Minima den Grenzwert
, fźr die Minima den Grenzwert ![]() .
.