Hans Walser, [20120706]

Das FIN-Rechteck

1 Ansetzen oder abschneiden

Einem DIN-Rechteck setzen wir an der Schmalseite ein Quadrat an oder schneiden ein Quadrat ab.

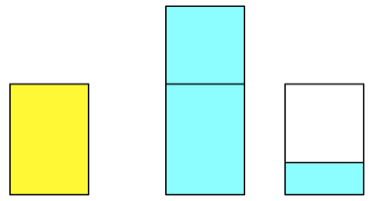
Ansetzen oder abschneiden

Im ersten Fall entsteht ein Gesamtrechteck mit dem Seitenverhältnis , im zweiten Fall bleibt ein Restrechteck mit dem Seitenverhältnis übrig. Dieses Restrechteck erhalten wir auch, wenn wir Papier im DIN-Format zu quadratischem Origami-Papier zuschneiden. Wegen

sind die beiden Rechtecke ähnlich. Wir bezeichnen ein Rechteck mit diesem Seitenverhältnis als FIN-Rechteck.

2 Abschneiden von zwei Quadraten

Wenn wir bei einem FIN-Rechteck zwei Quadrate abschneiden, bleibt wieder ein FIN-Rechteck übrig.

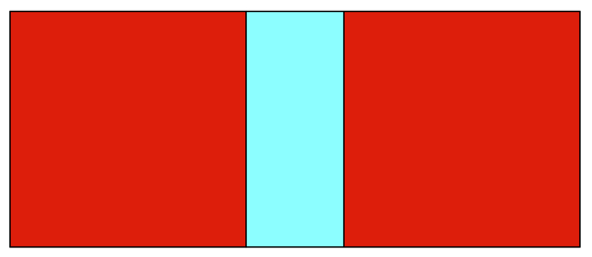
Abschneiden zweier Quadrate

Dieses Abschneiden von zwei Quadraten kann iteriert werden.

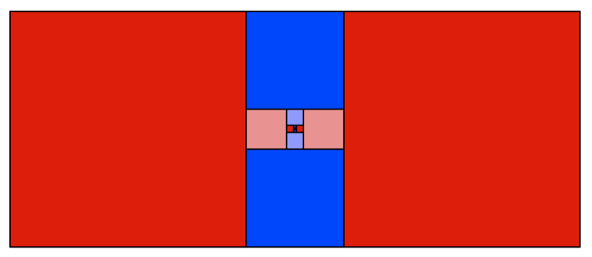
Iteration

Nun können wir zum Beispiel mit Spiralen verzieren, welche aus Viertelkreisen zusammengesetzt sind.

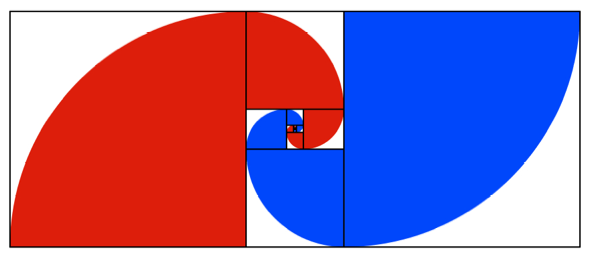
Spiralen

3 Ansetzen von zwei Quadraten

Natürlich hätten wir auch je zwei Quadrate ansetzen können. In der folgenden Abbildung wurden zunächst einfach einmal zwei Einheitsquadrate nebeneinander gesetzt. Dann wurden je zwei Quadrate angesetzt. So erhalten wir eine Folge von Rechtecken.

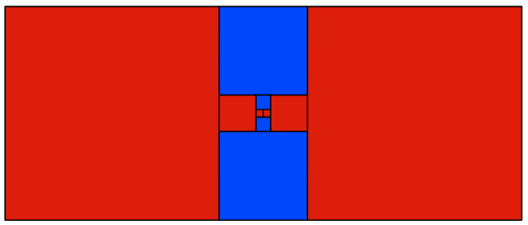
Bottom up

Für die Seitenlängen der Quadrate erhalten wir die Folge:

1, 2, 5, 12, 29, 70, ...

Dies sind die so genannten Pell-Zahlen mit der Rekursion:

Für deren Quotientenfolge erhalten wir den Grenzwert . Die Rechtecke nähern sich also dem Format des FIN-Rechtecks an.

4 Diagonalen im FIN-Rechteck

Die beiden Diagonalen im FIN-Rechteck schneiden sich unter einem spitzen Winkel von 45°.

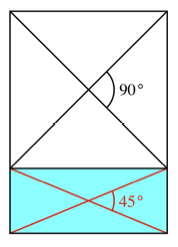
Diagonalenschnittwinkel 45°

Dies kann zunächst rechnerisch eingesehen werden: Für den spitzen Diagonalenschnittwinkel erhalten wir zunächst:

Damit wird:

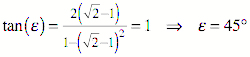
Einfacher ist eine geometrische Überlegung (mitgeteilt von Renato Pandi): Die Verbindungslinie der beiden Diagonalenschnittpunkte des Quadrates und des FIN-Rechtecks ist die halbe Langseite des DIN-Rechteckes, im Format also und damit gleich lang wie die halbe Quadratdiagonale. Somit ergeben sich die zwei in der Abbildung eingezeichneten gleichschenkligen Dreiecke mit dem Spitzenwinkel 45°.

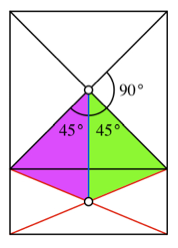
Zwei gleichschenklige Dreiecke

Die Basiswinkel dieser Dreiecke messen daher . So erhalten wir im FIN-Rechteck den stumpfen Diagonalenschnittwinkel 135°.

5 Regelmäßiges Achteck

Mit dem 45°-Winkel haben wir einen Link zum regelmäßigen Achteck.

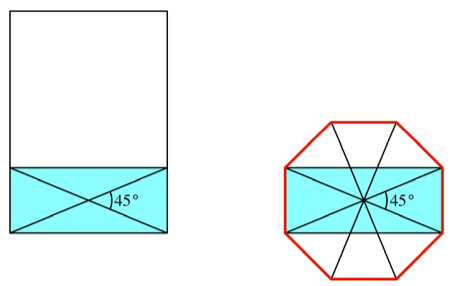
Link zum regelmäßigen Achteck

6 Flächeninhalt

Das regelmäßige Achteck hat den doppelten Flächeninhalt des FIN-Rechtecks. Dies kann auf verschiedene Weise eingesehen werden.

Zunächst einige Zerlegungsbeweise.

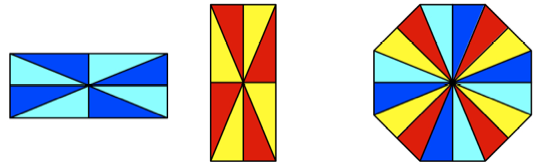
Zerlegungsbeweis mit 16 Puzzle-Teilen

Mit dem Stern aus Kindertagen geht es natürlich auch.

Stern

Es geht auch mit nur 8 Puzzle-Teilen.

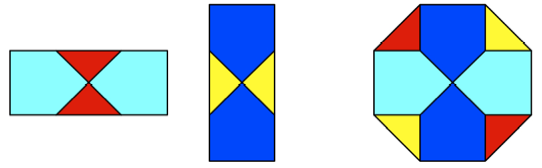
Zerlegungsbeweis mit 8 Puzzle-Teilen

Wir die Symmetrie eingeschränkt, geht es sogar mit nur 7 Puzzle-Teilen.

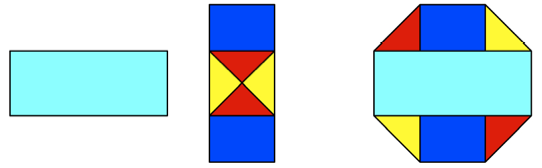
Zerlegungsbeweis mit 7 Puzzle-Teilen

Aus acht FIN-Rechtecken ergibt sich ein Achteck mit vierfachem Flächeninhalt.

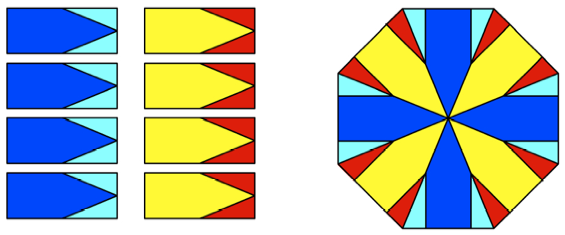
Zerlegungsbeweis

Bei Verzicht auf Axialsymmetrie kommen wir mit weniger Puzzle-Teilen durch.

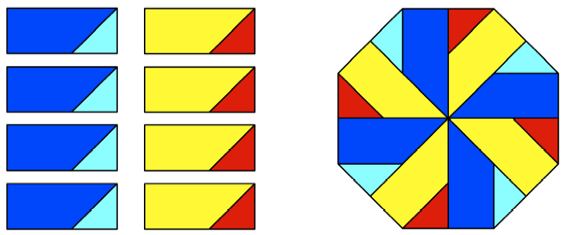
Zerlegungsbeweis

Und nun noch eine Kombination von Zerlegungsbeweis und Ergänzungsbeweis.

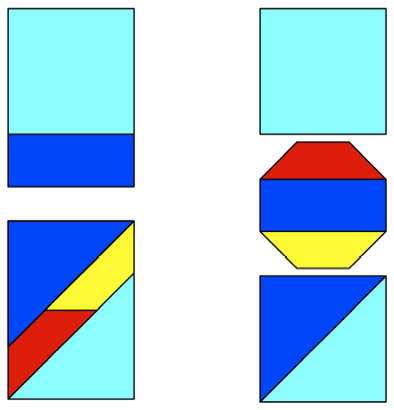
Stimmt es?

7 DIN-Rechteck und regelmäßiges Achteck

Die beiden in der Abbildung eingezeichneten gleichschenkligen Dreiecke machen flächenmäßig zusammen genau ein Viertel des DIN-Rechtecks aus.

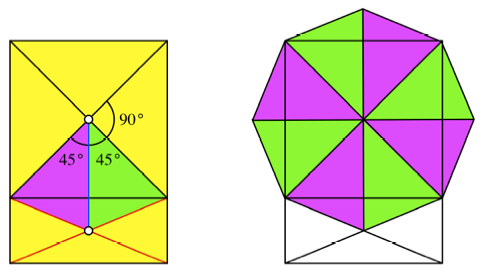
DIN-Rechteck und Achteck

Wir können daher zu einem Achteck ergänzen, welches zum DIN-Rechteck flächengleich ist.

Die folgende Abbildung zeigt einen Zerlegungsbeweis.

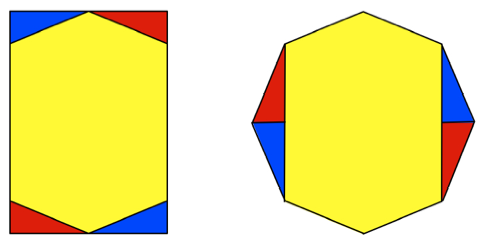
Zerlegung

8 Halbieren des DIN-Rechteckes

Die klassische Halbierung des DIN-Rechteckes geschieht durch die kurze Mittelparallele. Dadurch entstehen zwei Rechtecke wieder im DIN-Format.

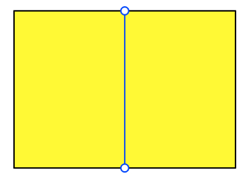
Klassische Halbierung

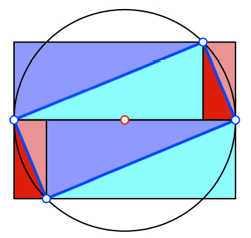
Es geht aber auch anders. Wir beschreiben dem DIN-Rechteck ein Rechteck mit zwei diametralen Ecken in den Mittelpunkten der Schmalseiten des DIN-Rechteckes ein. Die beiden anderen Ecken finden wir mit dem Thaleskreis.

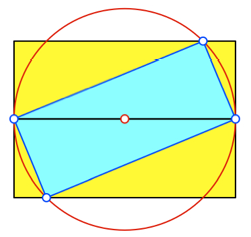
Einbeschriebenes Rechteck

Welches Format hat das einbeschriebene Rechteck? In einem DIN-Rechteck der Langseite und der Schmalseite 1 hat der Thaleskreis den Radius . Damit ergibt sich das in der Abbildung eingezeichnete rechtwinklig gleichschenklige Dreieck mit der Schenkellänge . Weiter sehen wir daraus, dass das einbeschriebene Rechteck den Diagonalenschnittwinkel 45° hat. Es ist also ein FIN-Rechteck.

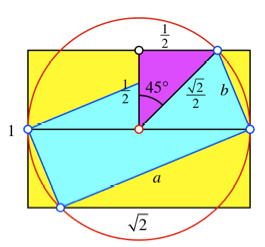
Maße

Für seine Seiten berechnen wir mit etwas Pythagoras:

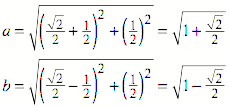
Daraus ergibt sich für den Flächeninhalt . Das Rechteck ist also flächenmäßig halb so groß wie das ursprüngliche DIN-Rechteck.

Das lässt sich auch durch Zerlegung zeigen.

Zerlegung

Das einbeschriebene FIN-Rechteck lässt sich auch durch einen Faltvorgang herstellen. Dabei spielt der 45°-Winkel eine wichtige Rolle.

Wir nehmen ein DIN-Papier, das auf der Vorderseite gelb und auf der Rückseite blau ist. Zur Vorbereitung führen wir die drei ersten Faltschritte des „Schiffchens“ oder der „Möwe“ durch und falten dann auf.

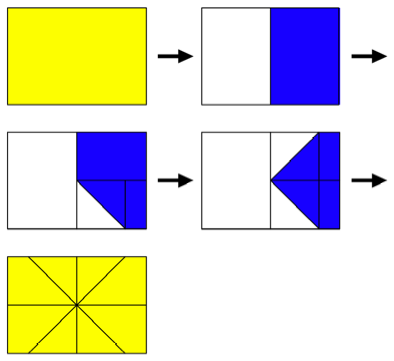
Faltvorbereitung

Nun können wir die Ecken des DIN-Rechteckes einfalten.

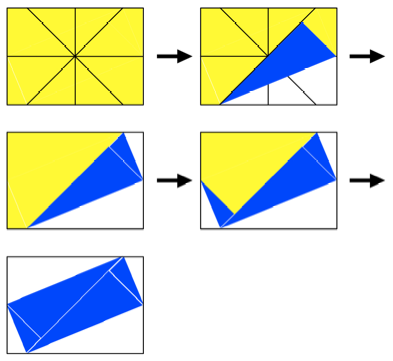
FIN-Rechteck

Das FIN-Rechteck ist überall zweilagig, es hat also den halben Flächeninhalt des ursprünglichen DIN-Rechteckes.

9 Bild des 4d-Hyperwürfels

Der Umriss eines gängigen 2d-Bildes des 4d-Hyperwürfel ist ein regelmäßiges Achteck. Daher finden wir das FIN-Rechteck an mehreren Orten.

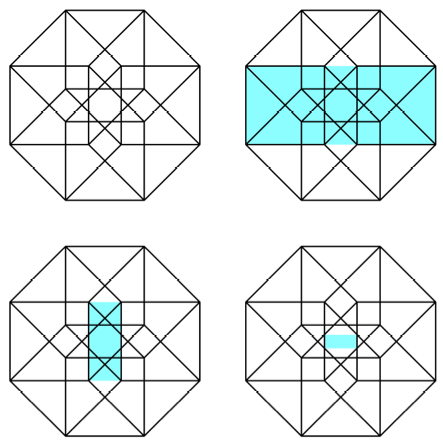
4d-Hyperwürfel

10 45°-Rhomben

Das Seitenmittenviereck des FIN-Rechtecks ist ein Rhombus mit Spitzenwinkeln 45°. Dies ist der kleinst-mögliche Rhombus, der einem FIN-Rechteck einbeschrieben werden kann.

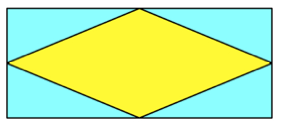
Kleinster 45°-Rhombus

Den größt-möglichen Rhombus erhalten wir durch Abschneiden zweier diametraler Ecken.

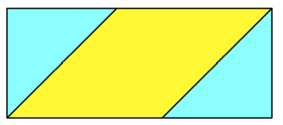
Größter 45°-Rhombus