Hans Walser, [20221013]

Fächer-Hyperwürfel

1     Worum geht es?

Zweidimensionale Darstellung des n-dimensionalen Hyperwürfels.

2     Grundidee

Wir arbeiten mit n fächerartig angeordneten Basisvektoren v1, v2, v3, ... , vn und benützen diese als Einheitsvektoren für Einheits-Hyperwürfel. Dann ergänzen wir zum Hyperwürfel. Durch Öffnen und Schließen des Fächers ergeben sich verschiedene Darstellungen.

3     Beispiele

Geordnet nach Dimensionen

3.1     Dimension 1. Gerade

Da ist nicht viel los.

Abb. 1: Dimension 1

3.2     Dimension 2. Ebene

Wir sehen Rhomben.

Abb. 2: Dimension 2

Ein Bild, das Platz enthält. Automatisch generierte Beschreibung

Abb. 2a: Quadrat. Wahres Bild

Abb. 2b: Spagat

3.3     Dimension 3. Raum

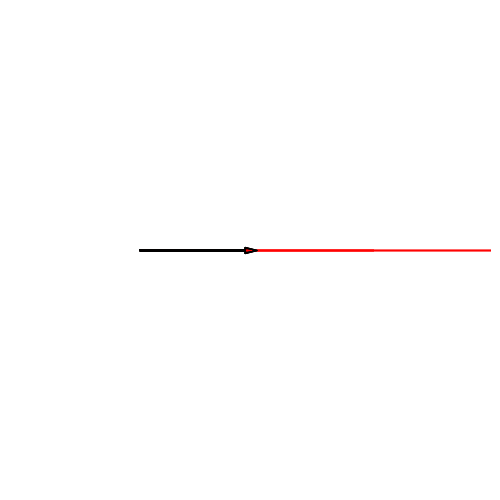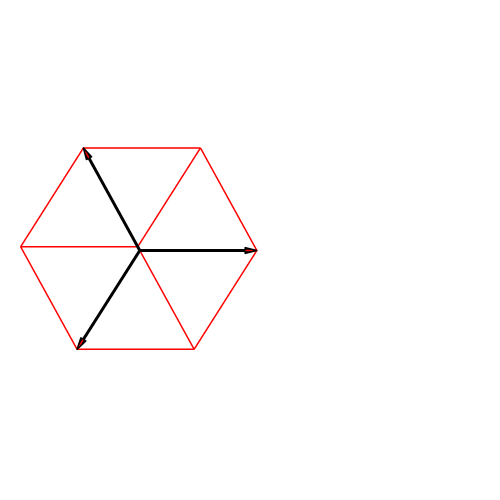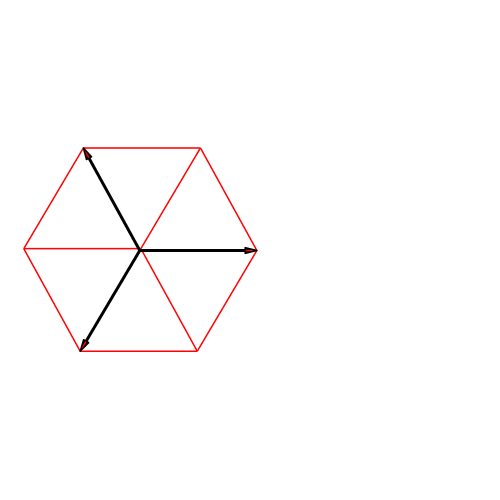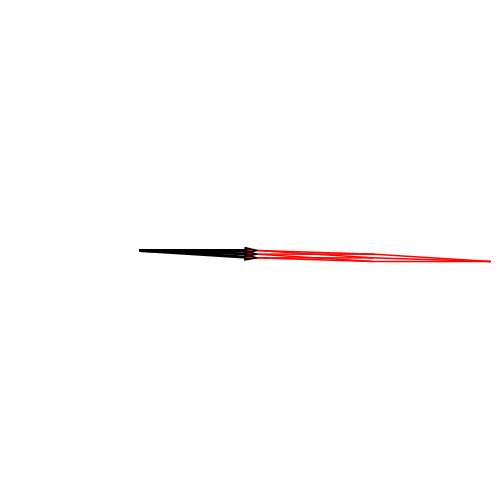
Abb. 3: Im Raum

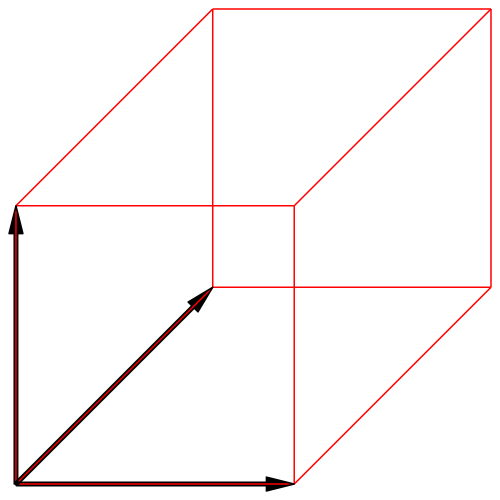
Abb. 3a: Würfel in Kavalierperspektive

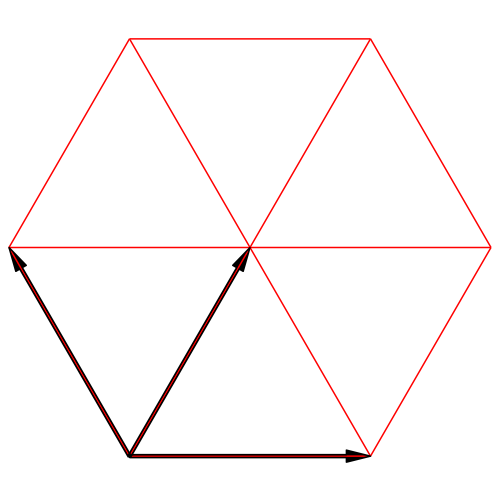
Abb. 3b: Würfel in isometrischer Darstellung

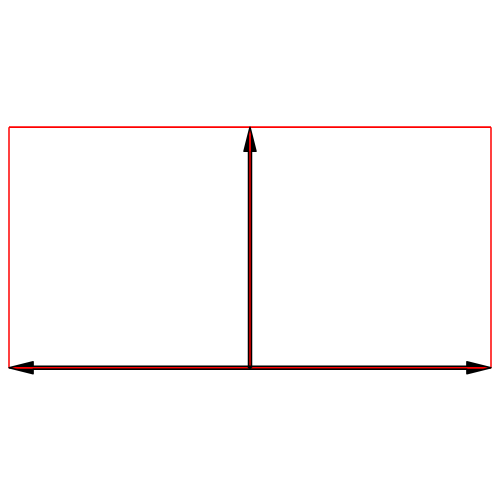
Abb. 3c: Verzerrte Sicht über eine Kante

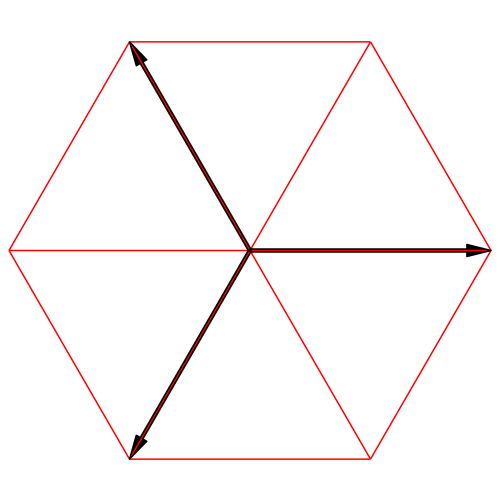
Abb. 3d: Nochmals isometrische Darstellung

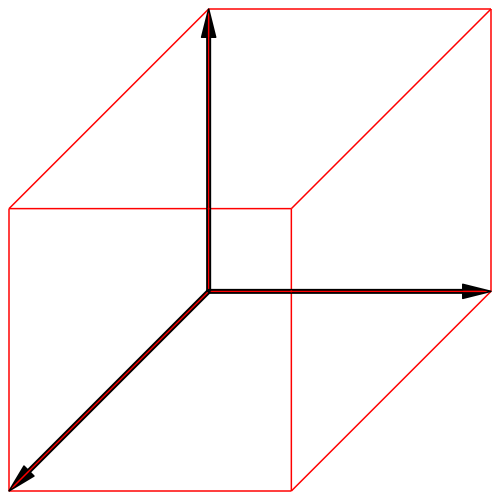
Abb. 3e: Nochmals Kavalierperspektive

3.4     Dimension 4. 4d-Hyperwürfel

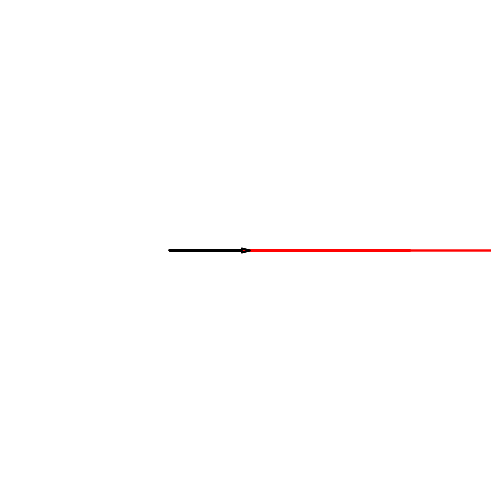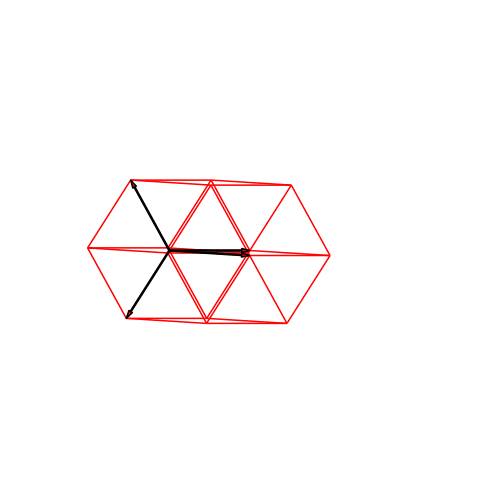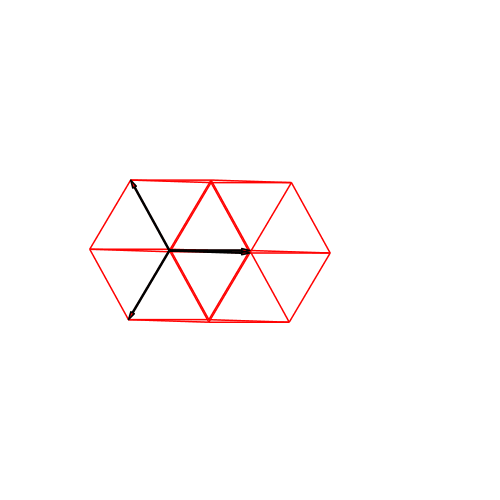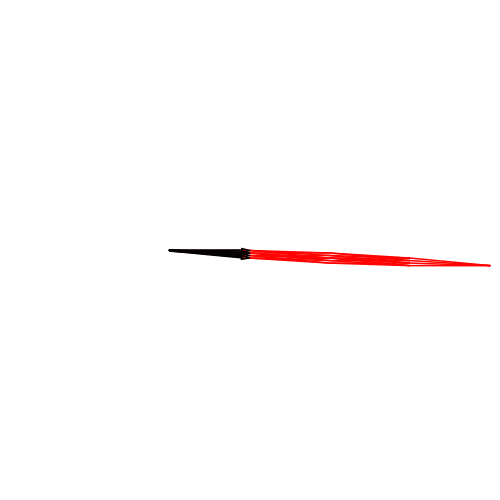
Abb. 4: 4d-Hyperwürfel

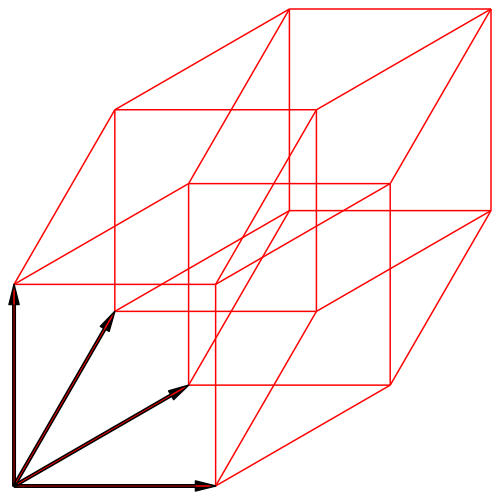
Abb. 4a: Kavalierperspektive

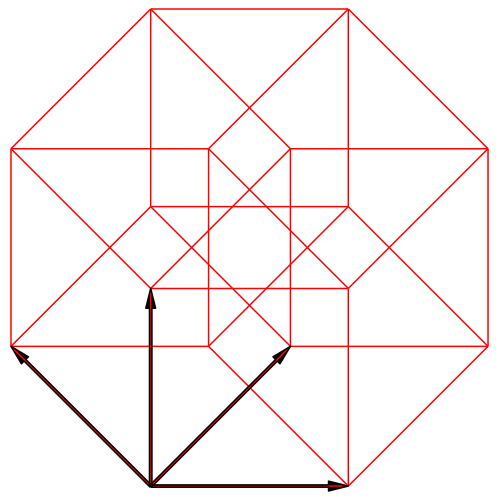
Abb. 4b: Klassisch

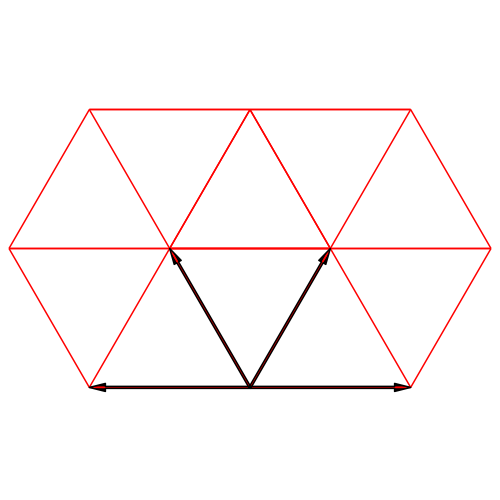
Abb. 4c: Dreiecksraster

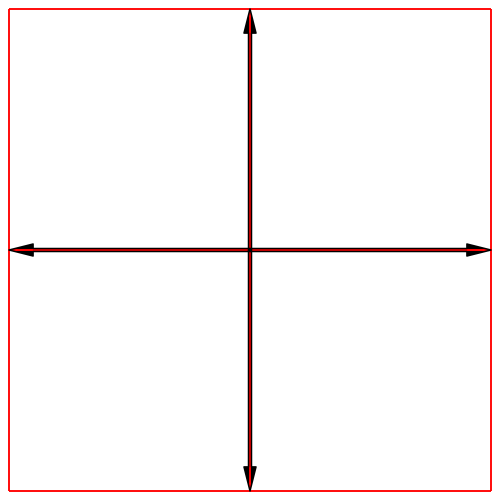
Ein Bild, das Gebäude enthält. Automatisch generierte Beschreibung

Abb. 4d: Quadratraster

3.5     5d-Hyperwürfel

Abb. 5: 5d-Hyperwürfel

Abb. 5a: Sonderfälle

3.6     6d-Hyperwürfel

Abb. 6: 6d-Hyperwürfel. Sonderfälle

4     Quer durch die Dimensionen

Die Abbildung 7 zeigt die Fächervergrößerung von 1 bis 7.

Abb. 7: Fächervergrößerung

 

Weblinks

 

Hans Walser: Diagonalen im Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/D/Diagonalen_im_Hyperwuerfel/Diagonalen_im_Hyperwuerfel.html

 

Hans Walser: Eckennummerierung von Hyperwürfeln

http://www.walser-h-m.ch/hans/Miniaturen/E/Eckennummerierung/Eckennummerierung.html

 

Hans Walser: Hypercubus

http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel/Hyperwuerfel.pdf

 

Hans Walser: Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel4/Hyperwuerfel4.html

 

Hans Walser: Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel3/Hyperwuerfel3.html

 

Hans Walser: Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel2/Hyperwuerfel2.htm

 

Hans Walser: Kollineare Punkte

http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte6/Kollineare_Punkte6.html

 

Hans Walser: Linsenträger Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/L/Linsentraeger-Hyperwuerfel/Linsentraeger-Hyperwuerfel.html

 

Hans Walser: Simplex

http://www.walser-h-m.ch/hans/Miniaturen/S/Simplex2/Simplex2.html