Hans Walser, [20200621]

Falsche Parabeln

1 Worum geht es?

Ein optischer Effekt mit Wellenlinien

2 Parabeln?

In der Abbildung 1 sehen wir eine Parabelschar. Jedenfalls meinen wir das. Die Parabeln, so es den welche sind, sind stehende, nach oben offene Parabeln.

Abb. 1: Parabelschar?

3 Wellenlinien

Die Figur ist aus gebogenen Wellenlinien aufgebaut, welche sich nicht berühren. Um dies einzusehen, zoomen wir in das in der Abbildung 2 eingetragene kleine blaue Quadrat hinein. Die Abbildung 3 zeigt den Zoom.

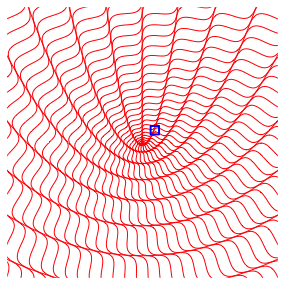
Abb. 2: Zoomquadrat

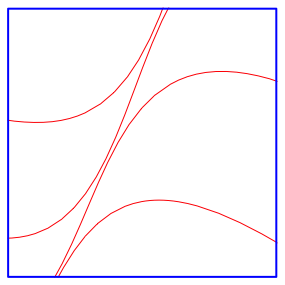
Abb. 3: Zoom

In der Abbildung 4 ist eine Wellenlinie blau hervorgehoben.

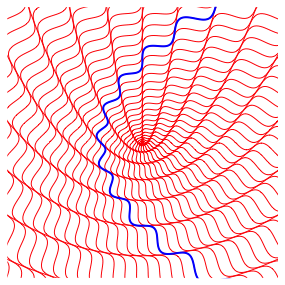
Abb. 4: Markierung einer Wellenlinie

Die Wellenlinie hat eine liegende Parabel als Mittellinie. In der Abbildung 1 sehen wir tatsächlich liegende, wellenlinienförmige Parabeln. Sie sind nach rechts offen.

4 Hintergrund

Die Figur der Abbildung 1 ist gebaut worden wie folgt. Wir beginnen mit einer Schar waagerechter Wellenlinien (Abb. 5a). Sie berühren sich nicht. Um dieses Nichtberühren einzusehen, zoomen wir in das kleine blaue Quadrat (Abb. 5b und 6).

In der Abbildung 5b sind auch noch zwei Wellenlinien mit den Mittellinien auf den Höhen und eingezeichnet sowie ein Quadratraster (blau / rot) mit der Maschenweite . Dies zum späteren Verständnis.

Die Wellenlinien haben die Parameterdarstellung:

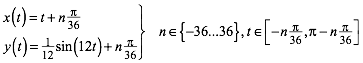(1)

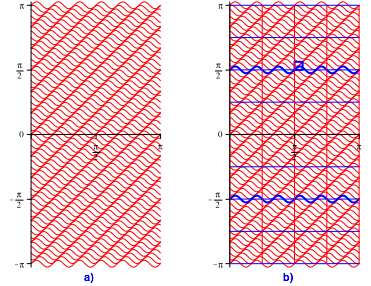
Abb. 5: Wellenlinien. Zoomquadrat

Abb. 6: Zoom

Nun transformieren wir die Situation der Abbildung 5b (ohne das Zoomquadrat) mit:

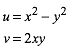(2)

Dies ist die reelle Darstellung der komplexen Quadratfunktion:

(3)

Mit dieser Transformation erhalten wir aus Der Figur der Abbildung 5b die Figur der Abbildung 7.

Man kann sich den Vorgang so vorstellen: Wir drehen in der Abbildung 5b die positive y-Achse um den Ursprung um +90° und die negative y-Achse um –90°. Zudem wird längenmäßig quadriert. Den Rest der Figur ziehen wir mit wie auf einer Gummihaut.

Exakte Formulierung: Wir denken jeden Punkt der Abbildung 5b in Polarkoordinaten. Nun quadrieren wir den Polarabstand und verdoppeln den Polarwinkel.

Die symmetrisch zur x-Achse liegenden blauen horizontalen Linien (Abb. 5b) vereinigen sich zu einer nach rechts offenen liegenden quadratischen Parabel.

Ebenso vereinigen sich die beiden blau markierten Wellenlinien zu einer durchgehenden Wellenlinie mit einer nach rechts offenen Parabel als Mittellinie.

Die senkrechten roten Linien werden zu nach links offenen quadratischen Parabeln. Das blau/rote Quadratraster wird zu einem aus Parabeln gebildeten Viereckraster. Die Vierecke sind näherungsweise Quadrate.

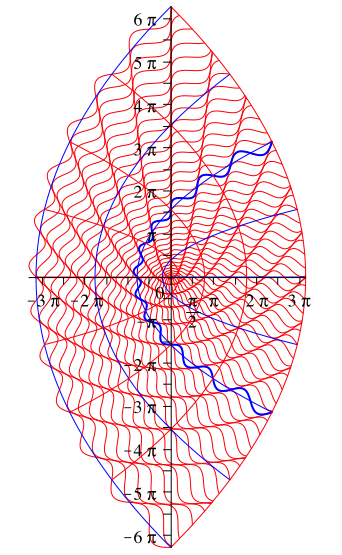
Abb. 7: Bild

Die Abbildung 1 ist ein Ausschnitt aus der Abbildung 7.

Websites

Hans Walser: Optische Täuschungen mit Sinuskurven

www.walser-h-m.ch/hans/Miniaturen/O/Opt_Taeuschung3/Opt_Taeuschung3.htm