Hans Walser, [20160531]

Falsche Perspektive

1 Worum geht es?

Die Abbildung 1 zeigt das Chorgitter in der ehemaligen Klosterkirche St. Ulrich, Kreuzligen. Dieses Chorgitter wurde 1737 vom Konstanzer Kunstschlosser Johann Jakob Hoffner geschaffen.

Stimmt die Perspektive?

Abb. 1: Chorgitter

Die Abbildung 2 zeigt einen Ausschnitt.

Abb. 2: Ausschnitt

2 Das Raster

In der Abbildung 2 sehen wir ein 12 × 9-Raster. Die Abbildung 3a zeigt dieses Raster entzerrt. In der Abbildung 3b sind eine Rasterdiagonale und ein Kreis eingezeichnet. Der Kreis hat den Radius 5. Er verläuft durch 12 Rasterpunkte (in der Abbildung 3b ist der zwölfte Rasterpunkt oberhalb des gezeichneten Rasters).

Wir nehmen an, dass das Raster ein Quadratraster ist. Das spielt aber keine wesentliche Rolle. Wir könnten unsere Überlegungen auch mit einem Rechteckraster durchführen. Der Kreis in der Abbildung 3b würde dann zu einer Ellipse.

Abb. 3: Quadratraster

3 Die Diagonalprobe

In der Abbildung 4 sind Punkte markiert, die auf einer Rasterdiagonalen liegen.

Abb. 4: Diagonale?

Bei einer korrekten Perspektive müssten diese Punkte auf einer Geraden liegen. Sie tun es nicht. Die Perspektive ist also falsch.

4 Die Kreisprobe

In der Abbildung 4 sind elf Rasterpunkte markiert, die gemäß Abbildung 3b auf einem Kreis liegen. Zudem ist der zugehörige Kreismittelpunkt markiert.

Abb. 5: Bild eines Kreises?

Das Ding hat ein eher birnenförmiges Aussehen. Es dürfte eher nicht das perspektivische Bild eines Kreises sein, ein Kegelschnitt also.

5 Rekonstruktion des Rasters

Wir versuchen, das Quadratraster zu rekonstruieren.

Die Abbildung 6 zeigt die in die Tiefe laufenden Linien, die so genannten Fluchtlinien.

Abb. 6: Fluchtlinien

Der Fluchtpunkt ist im Bauchnabel der Figur im zentralen Schrein.

Wir sehen allerdings, dass nicht alle Fluchtlinien im schmiedeeisernen Gitter stimmen. Wir haben teilweise Abweichungen gegen die Mitte hin.

Die horizontalen Gitterlinien finden wir nun mit Hilfe einer Diagonalen (Abb. 7).

Abb. 7: Horizontale Linien

6 Horizontlinie

Die Diagonalprobe stimmt nun und zeigt zudem, dass sich die Diagonalen in einem Punkt auf der Horizontlinie schneiden (Abb. 8).

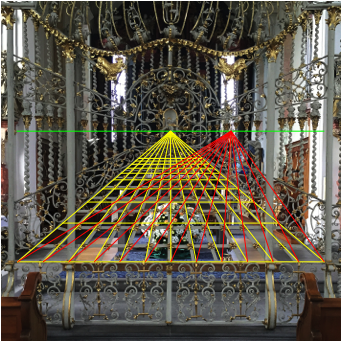
Abb. 8: Diagonalprobe

Die Rasterpunkte gemäß Abbildung 3b liegen auf eine Ellipse (Abb. 9). In unserem Beispiel ist die Ellipse beinahe ein Kreis.

Abb. 9: Ellipse