Hans Walser, [20200529]

Falsche Perspektive

1 Worum geht es?

Es wird diskutiert, ob die Perspektive in der Abbildung 1 stimmt.

Abb. 1: Sonne am Wolfgangsee (Foto durch den Autor)

Das Bild befindet sich an der Außenwand der Mensa im Bifeb (Bundesinstitut für Erwachsenenbildung, Bürglstein 1–7, A-5360 St. Wolfgang i.S.).

Anlässlich einer Geometrietagung am Bifeb wurde die Frage laut, ob in diesem Bild die Perspektive stimme.

Zur Bearbeitung dieser Frage gehen wir von der Annahme aus, dass das außerhalb der Sonne sichtbare Dreiecksmuster in ein perspektivisch dargestelltes Raster von kongruenten Rechtecken passt. Die Abbildung 2 zeigt ein solches hypothetisch angenommenes Rechteckraster.

Es werden einige Testmethoden besprochen.

Abb. 2: Hypothetisches Rechteckraster

2 Argumente gegen die Stimmigkeit der Perspektive

2.1 Diagonalentest

In einem Rechteckraster laufen die Diagonalen über Eck geradlinig weiter (Abb. 3).

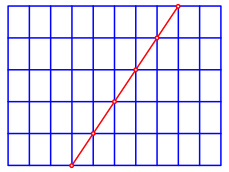
Abb. 3: Diagonale über Eck

Da eine perspektivische Abbildung geradenerhaltend ist, müsste das auch in unserem Bild (Abb. 1 und 2) gelten. Der Diagonalentest ist aber negativ, die Folge der Diagonalen ist leicht gekrümmt (Abb. 4).

Abb. 4: Diagonalentest negativ

Dieser Test ist sehr einfach und kann leicht vor Ort gemacht werden, indem zum Beispiel eine gerade Papierkante als Vergleichsobjekt dient.

Es gibt viele Beispiele von „Kunst am Bau“, die den Diagonalentest nicht bestehen. Perspektivische Chorschrankengitter in barocken Kirchen haben oft eine falsche Perspektive. Auch in etlichen Schulbüchern finden sich – Gott sei’s geklagt – solche falsche Perspektiven.

Zur Zeit von Albrecht Dürer (1471-1528) war die Perspektive noch eine echte Herausforderung (Schröder 1980). In frühen Bildern von Dürer finden sich noch falsche Perspektiven wie in der Abbildung 4. Später hat er dazugelernt.

Erinnerung: Wir sind von der Hypothese ausgegangen, dass das Rechteckraster aus kongruenten Rechtecken besteht, etwa wie ein Plattenboden aus gleichen rechteckigen Platten. Wenn die Rechtecke in der Tiefenrichtung zunehmend länger sein dürfen, sind natürlich auch bei einer korrekten Perspektive die Übereck-Diagonalen nicht auf einer Geraden.

2.2 Noch ein Diagonalentest

In einem perspektivischen Bild haben Parallelenscharen einen scheinbaren Schnittpunkt (wird manchmal Fernpunkt oder Fluchtpunkt genannt) auf der Horizontlinie. Das berühmte Beispiel dazu ist ein Foto von Eisenbahnschienen.

In unserm Bild haben die Tiefenlinien einen solchen scheinbaren Schnittpunkt. In der Abbildung 5 ist auch die Horizontlinie (grün) eingetragen.

Weiter sind horizontal jeweils zehn Rasterrechtecke zu einem großen Rechteck zusammengefasst und die Diagonalen dieser großen Rechtecke eingetragen. Diese Diagonalen sind in Wirklichkeit parallel, müssten sich also im Bild auf der grünen Horizontlinie schneiden.

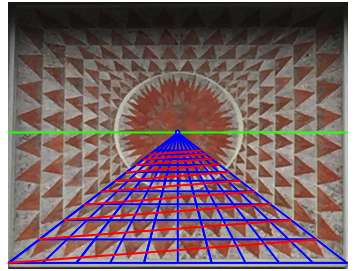
Abb. 5: Noch mehr Diagonalen

Tun sie aber nicht, sondern sind, horribile dictu, auch im Bild parallel. Test negativ.

Bemerkungen:

(1) Wir werden sogar das Opfer einer optischen Täuschung, indem wir die Bildgeraden nach rechts fächerförmig gespreizt sehen. Das ist so, weil unser perspektivisch geschultes Hirn erwartet, die Bildgeraden müssten nach rechts zu einem Schnittpunkt zusammenlaufen.

(2) Didaktische Bemerkung: Diese fälschlicherweise parallelen Bildgeraden liefern den Schlüssel zur Denkstruktur des Bildurhebers. Die breiten Rechtecke mit ihren Diagonalen bilden eine abnehmende geometrische Folge mit einem Grenzpunkt. Dieser Grenzpunkt wurde mit dem perspektivischen Fluchtpunkt verwechselt. Bei einer korrekten perspektivischen Darstellung haben wir es aber nicht mit einer abnehmenden geometrischen Folge (wie etwa der Zahlenfolge ) zu tun, sondern mit einer abnehmenden harmonischen Folge (wie etwa der Zahlenfolge ). — Kann sein, dass man die harmonische Folge scheut wie der Teufel das Weihwasser. Hat man doch auf der hohen Schul gelernt, dass die harmonische Reihe divergiert, wogegen die geometrische Reihe bei einem Reproduktionsfaktor unter 1 konvergiert. Aber es geht in unserem Kontext gar nicht um die Reihe, sondern um die Folge.

2.3 Kreistest

Im 10×10-Quadratraster gibt es den bekannten Zwölfpunktekreis (Abb. 6a). Hintergrund ist das Lehrerdreieck (rechtwinkliges Dreieck mit den Seitenlängen 3, 4, 5).

In einem Rechteckraster ergibt sich entsprechend eine Ellipse (Abb. 6b).

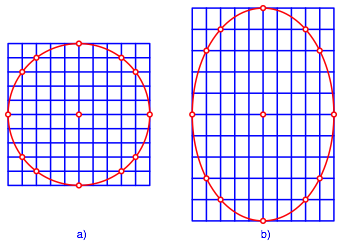
Abb. 6: Zwölfpunktekreis und Zwölfpunktellipse

In einer Perspektive ist das Bild eines Kegelschnittes wieder ein Kegelschnitt. In unserem Beispiel sind Ellipsen zu erwarten. In der Abbildung 7 wurde zunächst der Raster mit der falschen Methode der geometrischen Folge auf einen 10×10-Raster ausgedehnt und anschließend mit den 12 Punkten entsprechend der Abbildung 6 versehen.

Abb. 7: Keine Ellipse

Die Kurve durch diese zwölf Punkte kann wohl kaum als Ellipse angesehen werden. Sieht eher aus wie der Humpty Dumpty. Test erneut negativ.

3 Geometrischer Hintergrund

Für die folgenden Ausführungen siehe auch Walser (2018).

3.1 Korrekte und falsche Perspektive

Die Abbildung 8 zeigt eine korrekte Perspektive. Die Tiefenlinien verlaufen in den Fluchtpunkt.

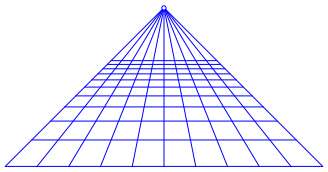
Abb. 8: Korrekte Perspektive

Ausgehend von einem kartesischen u,v-Netz erhalten wir das Netz der Abbildung 8 durch die gebrochen linearen Abbildungsgleichungen:

(1)

Der Parameter v im Nenner führt zu einer Tiefenstaffelung im Sinne einer harmonischen Folge.

Die Abbildung 9 zeigt eine falsche Perspektive. Die Abstände zwischen den Querlinien nehmen immer mit demselben Faktor ab. Die Tiefenlinien verlaufen ebenfalls in einen Fluchtpunkt.

Abb. 9: Falsche Perspektive

Das Netz der Abbildung 9 ist gegeben durch:

(2)

Der Parameter v in der Exponentialfunktion führt zu einer Tiefenstaffelung im Sinne einer geometrischen Folge.

3.2 Diagonalen

In einer korrekten Perspektive erscheint eine Folge von Übereck-Diagonalen als Gerade (Abb. 10).

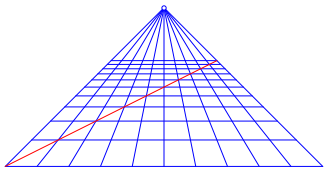
Abb. 10: Diagonalentest bei korrekter Perspektive

Alle zu dieser Diagonale parallelen Diagonalen verlaufen im Bild durch denselben Fluchtpunkt (Abb. 11).

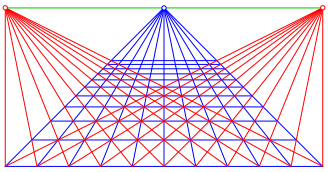
Abb. 11: Diagonalen-Fluchtpunkte

Die Konterdiagonalen haben ebenfalls einen Fluchtpunkt. Die Fluchtpunkte liegen auf der sogenannten Horizontlinie.

Bei der falschen Perspektive der Abbildung 9 entsteht beim Diagonalentest eine gekrümmte Kurve (Abb.12).

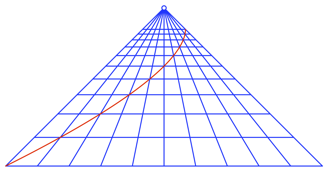
Abb. 12: Diagonalentest bei falscher Perspektive

Die Kurve und die dazu „parallelen“ Kurven laufen oben in den Fluchtpunkt (Abb. 13). Dasselbe tun die Konterkurven. Wir haben also keine Horizontlinie, sondern einen „Horizontpunkt“.

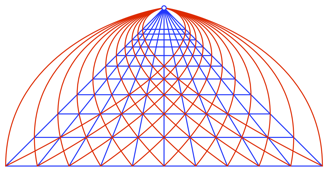
Abb. 13: Einmünden in den Fluchtpunkt

Wir besprechen exemplarisch die Diagonalkurve . Aus (2) erhalten wir:

(3)

Elimination des Parameters u führt auf:

(4)

Durch die Koordinatentransformation (entspricht einer Spiegelung an der Winkelhalbierenden des 2. und 4. Quadranten)

(5)

erhalten wir die einfache Form:

(6)

Die Abbildung 14 zeigt den zugehörigen Funktionsgrafen für .

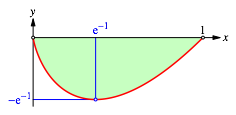
Abb. 14: Funktionsgraf

Die Funktion (6) ist ein dankbares Beispiel zur Kurvendiskussion und Integration.

Für den Tiefpunkt T erhalten wir:

(7)

Mit partieller Integration ergibt sich:

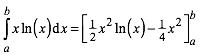(8)

Insbesondere:

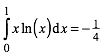(9)

Die Figur lässt sich zu einem Kleeblatt zusammensetzen (Abb. 15). Das Kleeblatt passt in den Einheitskreis. Wegen (9) hat es den Flächeninhalt 2.

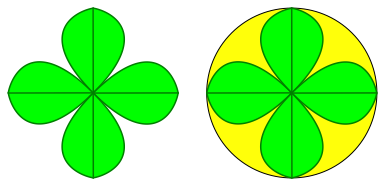
Abb. 15: Kleeblatt

3.3 Zwölfpunktellipse

Bei einer korrekten Zentralperspektive wird aus der Zwölfpunktellipse (Abb. 6) wieder eine Ellipse, die durch die entsprechenden Gitterpunktbilder verläuft (Abb. 16). Das Bild des Ellipsenmittelpunktes ist allerdings nicht der Mittelpunkt der Bildellipse.

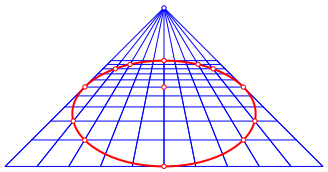
Abb. 16: Ellipse bei korrekter Perspektive

Bei einer falschen Perspektive ergibt sich der Humpty Dumpty (Abb. 7 und 17).

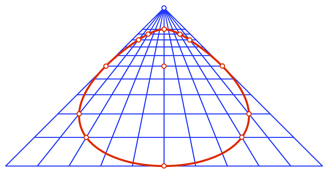
Abb. 17: Humpty Dumpty

Literatur

Schröder, Eberhard (1980): Dürer. Kunst und Geometrie. Dürers künstlerisches Schaffen aus der Sicht seiner »Underweysung«. Basel: Birkhäuser. ISBN 3-7643-1182-7.

Walser, Hans (2018): Falsche Perspektive. MNU Journal – Ausgabe 2.2018. S. 87-89. ISSN 0025-5866. 2

Website

Hans Walser: Falsche Perspektive

www.walser-h-m.ch/hans/Miniaturen/F/Falsche_Perspektive/Falsche_Perspektive.htm

Hans Walser: Kleeblatt

http://www.walser-h-m.ch/hans/Miniaturen/K/Kleeblatt/Kleeblatt.htm