Hans Walser, [20160524]
Falsche SchrŠgbilder
1 Worum geht es?
In einem Schulbuch wird im Zusammenhang mit der Einfźhrung des SchrŠgbildes die Figurenfolge der Abbildung 1 (Nachzeichnung durch den Autor) vorgestellt.
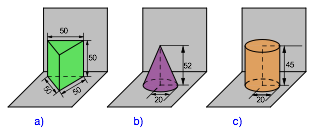
Abb. 1: SchrŠgbilder?
Im Kontext des Schulbuchtextes ist anzunehmen, dass es sich bei den Beispielen b) und c) um einen geraden Kreiskegel beziehungsweise einen geraden Kreiszylinder handelt.
2 Bearbeitung
2.1 Beispiel a)
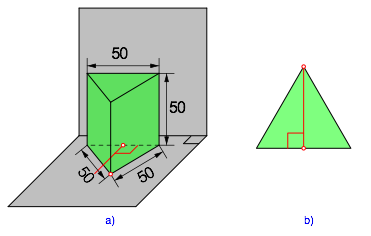
Abb. 2: Wo steckt der Fehler?
Auf Grund der Ma§angaben ist das Bodendreieck gleichseitig. In der Abbildung 2 ist zusŠtzlich eine Dreieckshšhe eingezeichnet. Diese mźsste durch die Spitze gehen.
Fehleranalyse:
á Mangelnde Kenntnisse der Geometrie des gleichseitigen Dreieckes.
á Mangelnde Kompetenzen der Technik des SchrŠgbildes.
á Mangelndes Raumgefźhl.
Die Abbildung 3 zeigt eine korrigierte Version.
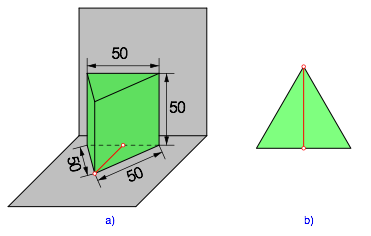
Abb. 3: Korrigierte Version
2.2 Beispiel b)
Wir zeichnen ein Umquadrat zur Bodenfigur (Abb. 4).
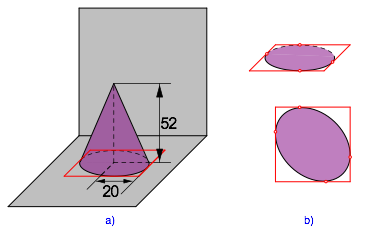
Abb. 4: Umquadrat
Die Bodenfigur berźhrt die Seiten des Umquadrates nicht in den Seitenmitten. Sie kann daher kein Kreis sein. Der im OriginalschrŠgbild gezeichnete Kegel hat in Wirklichkeit eine Ellipse als Grundfigur (Quetschkegel). Das passt aber nicht in den Kontext des Schulbuches.
Fehleranalyse:
á Vermischung von SchrŠgbild (Parallelprojektion) und Normalprojektion in derselben Zeichnung.
á Mangelnde Kenntnisse źber den Inkreis eines Quadrates.
á Mangelndes Raumgefźhl.
Die Abbildung 5 zeigt die korrigierte Version.
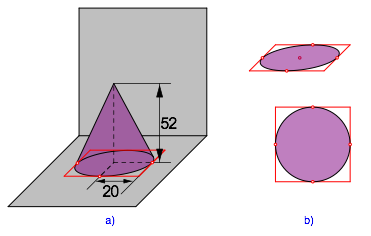
Abb. 5: Kreiskegel
Diese korrekte Fassung sieht ăunnatźrlichŇ aus. Das liegt im Wesen des SchrŠgbildes. Es verzerrt in einer Weise, die stark von der menschlichen Sehweise abweicht. Daher sollte man SchrŠgbilder vermeiden.
2.3 Beispiel c)
Grundfigur analog zum Beispiel b).
3 Normalprojektion
Die Abbildung 6 zeigt dieselben drei Kšrper in Normalprojektion.

Abb. 6: Normalprojektion