Hans Walser, [20140810b]

Falscher Beweis fźr den Satz des Pythagoras

1     Der ăBeweisŇ

Wir arbeiten mit einem rechtwinkligen Dreieck in der źblichen Bezeichnung.

Fźr den FlŠcheninhalt  gilt einerseits  und andererseits .

Vergleich ergibt:

                                                                                                                            (1)         

                                                                      

Nun legen wir das Dreieck in ein kartesisches Koordinatensystem gemŠ§ Abbildung 1.

 

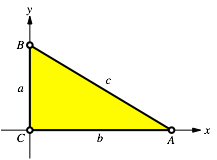
Abb. 1: Im Koordinatensystem

 

Die Gerade AB hat die Gleichung:

 

 

In der Hesseschen Normalform ergibt sich:

 

 

Die Gerade AB hat somit vom Ursprung C den Abstand:

 

 

Vergleich mit (1) ergibt .

 

2     Wo ist der Fehler?

In der Hesseschen Normalform steckt bereits der Satz des Pythagoras drin.