Hans Walser, [20210318]

Falscher Lösungsweg

Anregung: F. E., V.

1 Worum geht es?

Beispiel einer Aufgabe, bei der ein falscher Lösungsweg zur richtigen Lösung führt

2 Die Aufgabe

Ein Gleis wird durch die Funktion

(1)

beschrieben. Es endet an der Station und soll bis zur Station fortgesetzt werden (Abb. 1). Die Fortsetzung soll durch eine Polynomfunktion dritten Grades beschrieben werden. Bestimme diese Polynomfunktion. Bedenke, dass die beiden Funktionen an der Station A keinen Unterbruch (Stetigkeit) sowie gleiche Steigung (kein „Knick“) und gleiche Krümmung (kein „Ruck“) haben sollen.

Abb. 1: Situation

3 Der richtige Lösungsweg

Aus (1) ergibt sich:

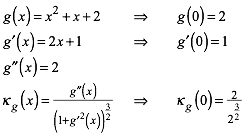(2)

Für die Polynomfunktion dritten Grades machen wir den Ansatz:

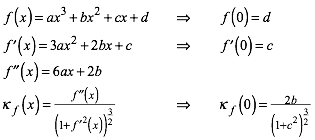(3)

Wegen dem glatten und ruckfreien Übergang in A erhalten wir aus (2) und (3) durch Vergleich:

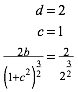(4)

Da der Graf der Polynomfunktion f durch verlaufen muss, gilt zusätzlich:

(5)

Die Bedingungen (4) und (5) bilden ein nichtlineares Gleichungssystem für a, b, c, d. Es ist allerdings sehr einfach zu lösen:

(6)

Die Nichtlinearität entsteht durch die Gleichheit der Krümmung im Übergangspunkt.

Die Abbildung 2 zeigt den Grafen der Lösung (rot).

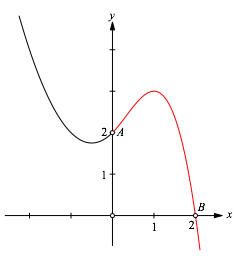
Abb. 2: Lösung

Die Abbildung 3 zeigt zusätzlich (blau) den gemeinsamen Krümmungskreis im Übergangspunkt A.

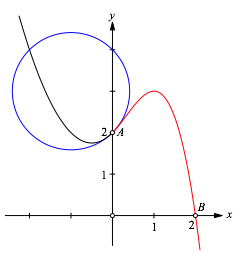
Abb. 3: Krümmungskreis

4 Der klassische Fehler

Nach einer nicht repräsentativen Umfrage bei meinen Geomatik-Studierenden an der ETH Zürich war etwa ein Viertel der falschen Meinung, die Krümmung sei die zweite Ableitung (analog zur Steigung, die durch die ersten Ableitung gegeben ist). Als (Gegen-)Beispiel dient die Parabel mit der Gleichung . Die zweite Ableitung ergibt die Konstante 2. Eine Kurve mit einer konstanten Krümmung ist aber ein Kreis.

(Bemerkung: Bei einer durch ihre eigene Bogenlänge parametrisierten Kurve ist die Länge des zweiten Ableitungsvektors tatsächlich betragsmäßig die Krümmung. Ein Funktionsgraf (mit Ausnahme der konstanten Funktion) ist aber nicht durch seine Bogenlänge parametrisiert.)

Diese Fehlvorstellung ist nicht die Folge einer Fehlüberlegung, sondern einer Fehlinstruktion.

Wie wirkt sich diese Fehlvorstellung bei unserer Aufgabe aus?

5 Falscher Lösungsweg

Statt der Krümmung der beiden Kurven müssen wir nun die zweiten Ableitungen gleichsetzen. Anstelle von (4) erhalten wir:

(4’)

Zusammen mit (5) erhalten wir nun ein lineares Gleichungssystem, das ebenfalls die Lösung (6) hat. Trotz der Fehlvorstellung ergibt sich die richtige Lösung.

6 Hintergrund

Aus der Krümmungsformel

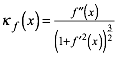(7)

folgt unmittelbar, dass bei Übereinstimmung der ersten und der zweiten Ableitung auch die Krümmung übereinstimmt. Wir können dann mit dem aus (4’) und (5) bestehenden linearen Gleichungssystem arbeiten.

7 Verkehrstechnische Bemerkungen

In unserem Beispiel haben wir sowohl in der Station A wie auch in der Station B eine Gleiskrümmung und damit gekrümmte Bahnsteige.

Ein Beispiel zu gekrümmten Bahnsteigen sind die Bahnsteige an den Geleisen 11 bis 16 im Obergeschoss des Berliner Hauptbahnhofes. Als Folge der durch die Gleiskrümmung erforderlichen Schrägstellung der Trasse sind die Bahnsteige gegenschräg, so dass bei nicht gesicherten Kinderwagen oder Rollkoffern ein Wegrollen auf das Geleise möglich ist.

Leider kann bei einer gekrümmten Gleisanlage im Bahnhof nicht einfach ein gerades Gleisstück eingebaut werde, da sich dadurch sowohl bei der Einfahrt wie bei der Ausfahrt in den Bahnhof ein Krümmungssprung ergäbe. Um dies zu vermeiden, müsste bei der Verwendung von Grafen von Polynomfunktionen mit Polynomfunktionen mindestens vierten Grades gearbeitet werden, so dass die Wendepunkte (dort haben wir keine Krümmung) in die Bahnhofsein- und -ausfahrten gelegt werden könnten.

In der Realität wird beim Gleisbau nicht mit Grafen von Polynomfunktionen gearbeitet sondern mit Klothoidenbögen. Klothoiden sind Kurven, bei denen die Krümmung proportional zur Bogenlänge zu- oder -abnimmt.

Die Abbildung 4 zeigt ein aus Klothoidenbögen zusammengesetztes Gleisoval.

Abb. 4: Klothoidenbögen