Hans Walser, [20120806]

Falscher Sinus

Anregung: [Hirscher 2012, S. 27]

Es werden Stroboskop-Effekte untersucht.

1        Eine falsche Sinuskurve

Die Funktion  hat eine recht hohe Frequenz:

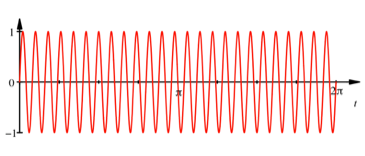
Abb. 1:

Wenn wir dieselbe Funktion mit der SchrittlŠnge  zeichnen, sieht sie aus wie die gewšhnliche Sinuskurve:

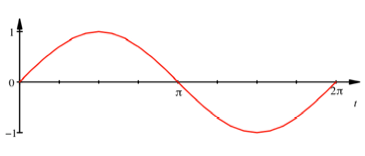
Abb. 2: Was ist hier los?

Um dies zu verstehen, heben wir Kurvenpunkte im Schrittabstand  speziell hervor:

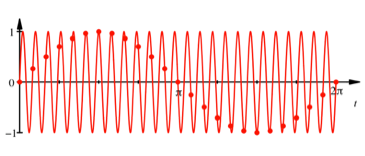
Abb. 3: Hervorgehobene Kurvenpunkte

Wir sehen, dass diese Punkte auf einer ăschšnenŇ Sinuskurve liegen.

In der Abbildung 2 haben wir tatsŠchlich keine echte Sinuskurve, sondern einen Polygonzug mit den Ecken in den Punkten der Abbildung 3. Diese Punkte werden gradlinig verbunden, was man bei genauem Hinsehen auch sieht.

2        Hintergrund

In der Funktion  setzen wir fźr t den Wert  ein. Damit ist:

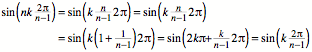
Der Kurvenpunkt mit der x-Koordinate  liegt also auch auf der gewšhnlichen Sinuskurve. Der eigentliche Hintergrund ist die 2ą-PeriodizitŠt der Sinus-Funktion.

3        Lissajous-Figuren

Die Kurve mit der Parameterdarstellung:

sieht prŠchtig aus (Abb. 4). Es ist dies eine so genannte Lissajous-Figur.

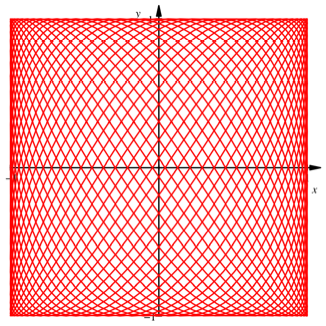
Abb. 4: Lissajous-Figur

Dieselbe Figur mit der SchrittlŠnge  gezeichnet ergibt ein regelmŠ§iges Zwšlfeck (Abb. 5).

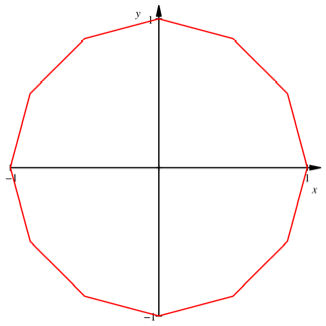
Abb. 5: SchrittlŠnge   

Die Punkte auf der Lissajous-Figur zur SchrittlŠnge  liegen in regelmŠ§igen AbstŠnden auf dem Einheitskreis (Abb. 6).

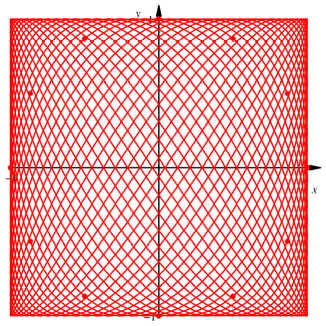
Abb. 6: Punkte auf der Kurve

Allgemein: Fźr die Lissajous-Figur mit der Parameterdarstellung

erhalten wir mit der SchrittlŠnge  ein regelmŠ§iges Vieleck mit  Eckpunkten auf dem Einheitskreis.

Literatur

[Hirscher 2012]          Hirscher, Horst: Medienbildung versus Computereinsatz? GDM-Mitteilungen 93, 2012, S. 23-28.